题目内容
(本小题满分14分)
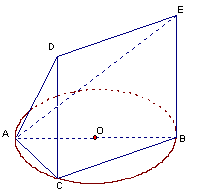 如图,△ABC内接于圆O,AB是圆O的直径,
如图,△ABC内接于圆O,AB是圆O的直径,![]() ,
,![]() ,设AE与平面ABC所成的角为
,设AE与平面ABC所成的角为![]() ,且
,且![]() ,四边形DCBE为平行四边形,DC
,四边形DCBE为平行四边形,DC![]() 平面ABC.
平面ABC.
(1)求三棱锥C-ABE的体积;
(2)证明:平面ACD![]() 平面
平面![]() ;
;
(3)在CD上是否存在一点M,使得MO//平面![]() ?
?
证明你的结论.
解:(1)∵四边形DCBE为平行四边形 ∴![]()
∵ DC![]() 平面ABC ∴
平面ABC ∴![]() 平面ABC
平面ABC
∴![]() 为AE与平面ABC所成的角,即
为AE与平面ABC所成的角,即![]() =
=![]() --------------------2分
--------------------2分
在Rt△ABE中,由![]() ,
,![]() 得
得![]() ------------3分
------------3分
∵AB是圆O的直径 ∴![]() ∴
∴![]()
![]() ∴
∴![]() ----------------------------------------4分
----------------------------------------4分
∴![]()
![]() ------------------5分
------------------5分
(2)证明:∵ DC![]() 平面ABC ,
平面ABC ,![]() 平面ABC ∴
平面ABC ∴![]() . --------------------6分
. --------------------6分
∵![]() 且
且![]() ∴
∴![]()
![]() 平面ADC.
平面ADC.
∵DE//BC ∴![]()
![]() 平面ADC ---------------------------------------8分
平面ADC ---------------------------------------8分
又∵![]() 平面ADE ∴平面ACD
平面ADE ∴平面ACD![]() 平面
平面![]() --------9分
--------9分
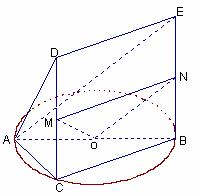 (3)在CD上存在点
(3)在CD上存在点![]() ,使得MO
,使得MO![]() 平面
平面![]() ,该点
,该点![]() 为
为![]() 的中点.------------10分
的中点.------------10分
证明如下:
如图,取![]() 的中点
的中点![]() ,连MO、MN、NO,
,连MO、MN、NO,
∵M、N、O分别为CD、BE、AB的中点,
∴.![]() ----------------------------------------------11分
----------------------------------------------11分
∵![]() 平面ADE,
平面ADE,![]() 平面ADE,
平面ADE,
∴![]() ------------------------------------------------------12分
------------------------------------------------------12分
同理可得NO//平面ADE.
∵![]() ,∴平面MNO//平面ADE.--------------------13分
,∴平面MNO//平面ADE.--------------------13分
∵![]() 平面MNO,∴MO//平面ADE. -------------14分(其它证法请参照给分)
平面MNO,∴MO//平面ADE. -------------14分(其它证法请参照给分)

 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)