题目内容
【题目】学校有线网络同时提供A、B两套校本选修课程。A套选修课播40分钟,课后研讨20分钟,可获得学分5分B套选修课播32分钟,课后研讨40分钟,可获学分4分。全学期20周,网络每周开播两次,每次均为独立内容。学校规定学生每学期收看选修课不超过1400分钟,研讨时间不得少于1000分钟。两套选修课怎样合理选择,才能获得最好学分成绩?
【答案】答案见解析.
【解析】试题分析:设选择![]() 两套课程分别为
两套课程分别为![]() 次,
次, ![]() 为学分,根据两套选修课所得学分可得目标函数
为学分,根据两套选修课所得学分可得目标函数![]() ,根据学校规定学生每学期收看选修课不超过
,根据学校规定学生每学期收看选修课不超过![]() 分钟,研讨时间不得少于
分钟,研讨时间不得少于![]() 分钟及
分钟及![]() 为正数,可得表示约束条件的二元一次不等式组,画出可行域,平移目标函数所表示的直线,结合最优解为整数点,可得最优解,从而可得结果.
为正数,可得表示约束条件的二元一次不等式组,画出可行域,平移目标函数所表示的直线,结合最优解为整数点,可得最优解,从而可得结果.
试题解析:设选择A、B两套课程分别为X、Y次,z为学分,
则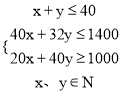 目标函数
目标函数 ![]()
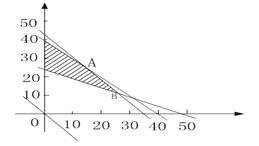
由方程组解得点A(15,25) , B(25,12.5)
由于目标函数的斜率与直线AB的斜率相等,因此在图中阴影线段AB上的整数点A(15,25)、C(19,20)、D(23,15)都符合题意,使得学分最高为175分。

练习册系列答案
相关题目

