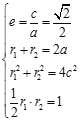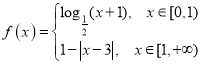题目内容
【题目】已知函数![]() 在点
在点![]() 处切线的斜率为1.
处切线的斜率为1.
(1)求![]() 的值;
的值;
(2)设![]() ,若对任意
,若对任意![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)-1;(2)![]() .
.
【解析】
(1)由题意,求得函数的导数![]() ,由
,由![]() ,即
,即![]() ,即可求解
,即可求解![]() 的值.
的值.
(2)由对任意![]() ,都有
,都有![]() ,转化为对任意
,转化为对任意![]() ,都有
,都有![]() ,设
,设![]() ,利用导数求得函数
,利用导数求得函数![]() 在
在![]() 上单调性,可得
上单调性,可得![]() ,设
,设![]() ,利用导数求得函数
,利用导数求得函数![]() 的单调性与最值,进而可得到答案.
的单调性与最值,进而可得到答案.
(1)由题意得,![]() ,
,
由于![]() ,所以
,所以![]() ,即
,即![]() .
.
(2)由题意得,当![]() 时,
时,![]() ,则有
,则有![]() .
.
下面证当![]() 时,对任意
时,对任意![]() ,都有
,都有![]() .
.
由于![]() 时,
时,![]() ,当
,当![]() 时,则有
时,则有![]() .
.
只需证明对任意![]() ,都有
,都有![]() .
.
证明:设![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上单调递增;
上单调递增;
所以当![]() 时,
时,![]() ,即
,即![]() ,
,
所以![]() ,则
,则![]() .
.
设![]() ,
,![]() ,则
,则![]() .
.
设![]() ,
,![]() ,则
,则![]() .
.
由于当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
则当![]() 时,
时,![]() .
.
又![]() 时,
时,![]() ,所以当
,所以当![]() 时,则
时,则![]() ,所以
,所以![]() 在
在![]() 上单调递增.
上单调递增.
当![]() 时,则
时,则![]() ,即
,即![]() ,所以
,所以![]() 在
在![]() 上单调递增.
上单调递增.
当![]() 时,则
时,则![]() .
.
所以对任意![]() ,都有
,都有![]() .
.
所以,当![]() 时,对任意
时,对任意![]() ,都有
,都有![]() .
.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目