ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ“―÷ΣΆ÷‘≤CΘΚ![]() Θ®aΘΨbΘΨ0Θ©ΒΡΉσΓΔ”“ΫΙΒψΖ÷±πΈΣF1Θ§F2Θ§«“άκ–Ρ¬ ΈΣ
Θ®aΘΨbΘΨ0Θ©ΒΡΉσΓΔ”“ΫΙΒψΖ÷±πΈΣF1Θ§F2Θ§«“άκ–Ρ¬ ΈΣ![]() Θ§MΈΣΆ÷‘≤…œ»Έ“β“ΜΒψΘ§Β±ΓœF1MF2ΘΫ90Γψ ±Θ§ΓςF1MF2ΒΡΟφΜΐΈΣ1Θ°
Θ§MΈΣΆ÷‘≤…œ»Έ“β“ΜΒψΘ§Β±ΓœF1MF2ΘΫ90Γψ ±Θ§ΓςF1MF2ΒΡΟφΜΐΈΣ1Θ°
Θ®ΔώΘ©«σΆ÷‘≤CΒΡΖΫ≥ΧΘΜ
Θ®ΔρΘ©“―÷ΣΒψA «Ά÷‘≤C…œ“λ”ΎΆ÷‘≤ΕΞΒψΒΡ“ΜΒψΘ§―”≥Λ÷±œΏAF1Θ§AF2Ζ÷±π”κΆ÷‘≤ΫΜ”ΎΒψBΘ§DΘ§…η÷±œΏBDΒΡ–±¬ ΈΣk1Θ§÷±œΏOAΒΡ–±¬ ΈΣk2Θ§«σ÷ΛΘΚk1ΓΛk2Β»”ΎΕ®÷ΒΘ°
ΓΨ¥πΑΗΓΩΘ®ΔώΘ©![]() Θ®ΔρΘ©ΦϊΫβΈω
Θ®ΔρΘ©ΦϊΫβΈω
ΓΨΫβΈωΓΩ
Θ®ΔώΘ©”…Χβ“βΩ…«σΒΟ![]() Θ§‘ρ
Θ§‘ρ![]() Θ§Ά÷‘≤
Θ§Ά÷‘≤![]() ΒΡΖΫ≥ΧΈΣ
ΒΡΖΫ≥ΧΈΣ![]() .
.
Θ®ΔρΘ©…η![]() Θ§
Θ§![]() Θ§
Θ§
Β±÷±œΏ![]() ΒΡ–±¬ ≤Μ¥φ‘ΎΜρ÷±œΏ
ΒΡ–±¬ ≤Μ¥φ‘ΎΜρ÷±œΏ![]() ΒΡ–±¬ ≤Μ¥φ‘Ύ ±Θ§
ΒΡ–±¬ ≤Μ¥φ‘Ύ ±Θ§![]() .
.
Β±÷±œΏ![]() ΓΔ
ΓΔ![]() ΒΡ–±¬ ¥φ‘Ύ ±Θ§
ΒΡ–±¬ ¥φ‘Ύ ±Θ§![]() ,…η÷±œΏ
,…η÷±œΏ![]() ΒΡΖΫ≥ΧΈΣ
ΒΡΖΫ≥ΧΈΣ![]() Θ§ΝΣΝΔ÷±œΏΖΫ≥Χ”κΆ÷‘≤ΖΫ≥ΧΘ§ΫαΚœΈΛ¥οΕ®άμΦΤΥψΩ…ΒΟ÷±œΏ
Θ§ΝΣΝΔ÷±œΏΖΫ≥Χ”κΆ÷‘≤ΖΫ≥ΧΘ§ΫαΚœΈΛ¥οΕ®άμΦΤΥψΩ…ΒΟ÷±œΏ![]() ΒΡ–±¬ ΈΣ
ΒΡ–±¬ ΈΣ![]() Θ§÷±œΏ
Θ§÷±œΏ![]() ΒΡ–±¬ ΈΣ
ΒΡ–±¬ ΈΣ![]() Θ§‘ρ
Θ§‘ρ![]() .Ήέ…œΩ…ΒΟΘΚ÷±œΏ
.Ήέ…œΩ…ΒΟΘΚ÷±œΏ![]() ”κ
”κ![]() ΒΡ–±¬ ÷°ΜΐΈΣΕ®÷Β
ΒΡ–±¬ ÷°ΜΐΈΣΕ®÷Β![]() .
.
Θ®ΔώΘ©…η![]() ”…Χβ
”…Χβ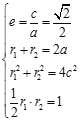 Θ§
Θ§
ΫβΒΟ![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§![]() Ά÷‘≤
Ά÷‘≤![]() ΒΡΖΫ≥ΧΈΣ
ΒΡΖΫ≥ΧΈΣ![]() .
.
Θ®ΔρΘ©…η![]() Θ§
Θ§![]() Θ§Β±÷±œΏ
Θ§Β±÷±œΏ![]() ΒΡ–±¬ ≤Μ¥φ‘Ύ ±Θ§
ΒΡ–±¬ ≤Μ¥φ‘Ύ ±Θ§
…η![]() Θ§‘ρ
Θ§‘ρ![]() Θ§÷±œΏ
Θ§÷±œΏ![]() ΒΡΖΫ≥ΧΈΣ
ΒΡΖΫ≥ΧΈΣ![]() ¥ζ»κ
¥ζ»κ![]() Θ§
Θ§
Ω…ΒΟ![]()
![]() Θ§
Θ§![]() Θ§‘ρ
Θ§‘ρ![]() ,
,
![]() ÷±œΏ
÷±œΏ![]() ΒΡ–±¬ ΈΣ
ΒΡ–±¬ ΈΣ Θ§÷±œΏ
Θ§÷±œΏ![]() ΒΡ–±¬ ΈΣ
ΒΡ–±¬ ΈΣ![]() Θ§
Θ§
![]() Θ§
Θ§
Β±÷±œΏ![]() ΒΡ–±¬ ≤Μ¥φ‘Ύ ±Θ§Ά§άμΩ…ΒΟ
ΒΡ–±¬ ≤Μ¥φ‘Ύ ±Θ§Ά§άμΩ…ΒΟ![]() .
.
Β±÷±œΏ![]() ΓΔ
ΓΔ![]() ΒΡ–±¬ ¥φ‘Ύ ±Θ§
ΒΡ–±¬ ¥φ‘Ύ ±Θ§![]() …η÷±œΏ
…η÷±œΏ![]() ΒΡΖΫ≥ΧΈΣ
ΒΡΖΫ≥ΧΈΣ![]() Θ§
Θ§
‘ρ”… œϊ»Ξ
œϊ»Ξ![]() Ω…ΒΟΘΚ
Ω…ΒΟΘΚ![]() Θ§
Θ§
”÷![]() Θ§‘ρ
Θ§‘ρ![]() Θ§¥ζ»κ…œ ωΖΫ≥ΧΩ…ΒΟ:
Θ§¥ζ»κ…œ ωΖΫ≥ΧΩ…ΒΟ:
![]() Θ§
Θ§![]() Θ§
Θ§
‘ρ![]()
![]() Θ§
Θ§
…η÷±œΏ![]() ΒΡΖΫ≥ΧΈΣ
ΒΡΖΫ≥ΧΈΣ![]() Θ§Ά§άμΩ…ΒΟ
Θ§Ά§άμΩ…ΒΟ![]() Θ§
Θ§
![]() ÷±œΏ
÷±œΏ![]() ΒΡ–±¬ ΈΣ
ΒΡ–±¬ ΈΣ
![]() ÷±œΏ
÷±œΏ![]() ΒΡ–±¬ ΈΣ
ΒΡ–±¬ ΈΣ![]() Θ§
Θ§![]()
 .
.
Υυ“‘Θ§÷±œΏ![]() ”κ
”κ![]() ΒΡ–±¬ ÷°ΜΐΈΣΕ®÷Β
ΒΡ–±¬ ÷°ΜΐΈΣΕ®÷Β![]() Θ§Φ¥
Θ§Φ¥![]() .
.
ΓΨΒψΨΠΓΩ
(1)Ϋβ¥π÷±œΏ”κΆ÷‘≤ΒΡΧβΡΩ ±Θ§ ±≥ΘΑ―ΝΫΗω«ζœΏΒΡΖΫ≥ΧΝΣΝΔΘ§œϊ»Ξx(Μρy)Ϋ®ΝΔ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΘ§»ΜΚσΫη÷ζΗυ”κœΒ ΐΒΡΙΊœΒΘ§≤ΔΫαΚœΧβ…ηΧθΦΰΫ®ΝΔ”–ΙΊ≤Έ±δΝΩΒΡΒ»ΝΩΙΊœΒΘ°
(2)…φΦΑΒΫ÷±œΏΖΫ≥ΧΒΡ…ηΖ® ±Θ§Έώ±ΊΩΦ¬«»ΪΟφΘ§≤Μ“ΣΚω¬‘÷±œΏ–±¬ ΈΣ0Μρ≤Μ¥φ‘ΎΒ»ΧΊ β«ι–ΈΘ°
ΓΨΧβ–ΆΓΩΫβ¥πΧβ
ΓΨΫα χΓΩ
21
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐfΘ®xΘ©ΘΫΘ®xΘΪbΘ©Θ®![]() Θ≠aΘ©Θ§Θ®bΘΨ0Θ©Θ§‘ΎΘ®Θ≠1Θ§fΘ®Θ≠1Θ©Θ©¥ΠΒΡ«–œΏΖΫ≥ΧΈΣΘ®eΘ≠1Θ©xΘΪeyΘΪeΘ≠1ΘΫ0Θ°
Θ≠aΘ©Θ§Θ®bΘΨ0Θ©Θ§‘ΎΘ®Θ≠1Θ§fΘ®Θ≠1Θ©Θ©¥ΠΒΡ«–œΏΖΫ≥ΧΈΣΘ®eΘ≠1Θ©xΘΪeyΘΪeΘ≠1ΘΫ0Θ°
Θ®ΔώΘ©«σaΘ§bΘΜ
Θ®ΔρΘ©»τΖΫ≥ΧfΘ®xΘ©ΘΫm”–ΝΫΗω Β ΐΗυx1Θ§x2Θ§«“x1ΘΦx2Θ§÷ΛΟςΘΚx2Θ≠x1Γή1ΘΪ![]() Θ°
Θ°
ΓΨ¥πΑΗΓΩΘ®ΔώΘ©![]() Θ§
Θ§![]() Θ®ΔρΘ©ΦϊΫβΈω
Θ®ΔρΘ©ΦϊΫβΈω
ΓΨΫβΈωΓΩ
Θ®ΔώΘ©”…Χβ“βάϊ”ΟΒΦΚ· ΐ―–ΨΩΚ· ΐΒΡ«–œΏΖΫ≥ΧΘ§ΒΟΒΫΙΊ”Ύa,bΒΡΖΫ≥ΧΉιΘ§«σΫβΖΫ≥ΧΉι≤ΔΦλ―ιΩ…ΒΟ![]() Θ§
Θ§![]() .
.
Θ®ΔρΘ©”…Θ®ΔώΘ©Ω…÷Σ![]() Θ§‘ρ
Θ§‘ρ![]() ‘Ύ(-1Θ§0)¥ΠΒΡ«–œΏΖΫ≥ΧΈΣ
‘Ύ(-1Θ§0)¥ΠΒΡ«–œΏΖΫ≥ΧΈΣ![]() Θ§ΙΙ‘λΚ· ΐ
Θ§ΙΙ‘λΚ· ΐ![]() Θ§ΫαΚœ–¬ΙΙ‘λΚ· ΐΒΡ–‘÷ Ζ÷άύΧ÷¬έΦ¥Ω…÷ΛΒΟΧβ÷–ΒΡ≤ΜΒ» Ϋ.
Θ§ΫαΚœ–¬ΙΙ‘λΚ· ΐΒΡ–‘÷ Ζ÷άύΧ÷¬έΦ¥Ω…÷ΛΒΟΧβ÷–ΒΡ≤ΜΒ» Ϋ.
Θ®ΔώΘ©”…Χβ“β![]() Θ§Υυ“‘
Θ§Υυ“‘![]() Θ§
Θ§
”÷![]() Θ§Υυ“‘
Θ§Υυ“‘![]() Θ§
Θ§
»τ![]() Θ§‘ρ
Θ§‘ρ![]() Θ§”κ
Θ§”κ![]() Ο§ΕήΘ§
Ο§ΕήΘ§
Ι ![]() Θ§
Θ§![]() .
.
Θ®ΔρΘ©”…Θ®ΔώΘ©Ω…÷Σ![]() Θ§
Θ§ ![]() Θ§
Θ§
…η![]() ‘Ύ(-1Θ§0)¥ΠΒΡ«–œΏΖΫ≥ΧΈΣ
‘Ύ(-1Θ§0)¥ΠΒΡ«–œΏΖΫ≥ΧΈΣ![]() Θ§“ΉΒΟΘ§
Θ§“ΉΒΟΘ§![]() Θ§
Θ§
Νν![]() Φ¥
Φ¥![]() Θ§
Θ§![]() Θ§
Θ§
Β±![]() ±Θ§
±Θ§![]() Θ§
Θ§
Β±![]() ±Θ§…η
±Θ§…η![]() Θ§
Θ§ ![]() Θ§
Θ§
Ι Κ· ΐ![]() ‘Ύ
‘Ύ![]() …œΒΞΒςΒί‘ωΘ§”÷
…œΒΞΒςΒί‘ωΘ§”÷![]() Θ§
Θ§
Υυ“‘Β±![]() ±Θ§
±Θ§![]() Θ§Β±
Θ§Β±![]() ±Θ§
±Θ§![]() Θ§
Θ§
Υυ“‘Κ· ΐ![]() ‘Ύ«χΦδ
‘Ύ«χΦδ![]() …œΒΞΒςΒίΦθΘ§‘Ύ«χΦδ
…œΒΞΒςΒίΦθΘ§‘Ύ«χΦδ![]() …œΒΞΒςΒί‘ωΘ§
…œΒΞΒςΒί‘ωΘ§
Ι ![]() .
.
![]() Θ§…η
Θ§…η![]() ΒΡΗυΈΣ
ΒΡΗυΈΣ![]() Θ§‘ρ
Θ§‘ρ![]() ”÷Κ· ΐ
”÷Κ· ΐ![]() ΒΞΒςΒίΦθΘ§
ΒΞΒςΒίΦθΘ§
Ι ![]() Θ§Ι
Θ§Ι ![]() Θ§
Θ§
…η![]() ‘Ύ(0,0)¥ΠΒΡ«–œΏΖΫ≥ΧΈΣ
‘Ύ(0,0)¥ΠΒΡ«–œΏΖΫ≥ΧΈΣ![]() Θ§
Θ§
“ΉΒΟ![]() Νν
Νν![]() Θ§
Θ§![]() Θ§
Θ§
Β±![]() ±Θ§
±Θ§![]() Θ§
Θ§
Β±![]() ±Θ§
±Θ§![]()
Ι Κ· ΐ![]() ‘Ύ
‘Ύ![]() …œΒΞΒςΒί‘ωΘ§”÷
…œΒΞΒςΒί‘ωΘ§”÷![]() Θ§
Θ§
Υυ“‘Β±![]() ±Θ§
±Θ§![]() Θ§Β±
Θ§Β±![]() ±Θ§
±Θ§![]() Θ§
Θ§
Υυ“‘Κ· ΐ![]() ‘Ύ«χΦδ
‘Ύ«χΦδ![]() …œΒΞΒςΒίΦθΘ§‘Ύ«χΦδ
…œΒΞΒςΒίΦθΘ§‘Ύ«χΦδ![]() …œΒΞΒςΒί‘ωΘ§
…œΒΞΒςΒί‘ωΘ§
![]() Θ§
Θ§![]()
…η![]() ΒΡΗυΈΣ
ΒΡΗυΈΣ![]() Θ§‘ρ
Θ§‘ρ![]() ”÷Κ· ΐ
”÷Κ· ΐ![]() ΒΞΒςΒί‘ωΘ§
ΒΞΒςΒί‘ωΘ§
Ι ![]() Θ§Ι
Θ§Ι ![]() Θ§
Θ§
”÷![]() Θ§
Θ§![]() .
.




