ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥Ή®¬τΒξœζ έ“Μ–¬ΩνΖΰΉΑΘ§»’œζ έΝΩΘ®ΒΞΈΜΈΣΦΰΘ©f(n) ”κ ±ΦδnΘ®1ΓήnΓή30ΓΔn![]() N*Θ©ΒΡΚ· ΐΙΊœΒ»γœ¬ΆΦΥυ ΨΘ§Τδ÷–Κ· ΐf(n) ΆΦœσ÷–ΒΡΒψΈΜ”Ύ–±¬ ΈΣ 5 ΚΆΘ≠3 ΒΡΝΫΧθ÷±œΏ…œΘ§ΝΫ÷±œΏΫΜΒψΒΡΚαΉχ±ξΈΣmΘ§«“ΒΎmΧλ»’œζ έΝΩΉν¥σ.
N*Θ©ΒΡΚ· ΐΙΊœΒ»γœ¬ΆΦΥυ ΨΘ§Τδ÷–Κ· ΐf(n) ΆΦœσ÷–ΒΡΒψΈΜ”Ύ–±¬ ΈΣ 5 ΚΆΘ≠3 ΒΡΝΫΧθ÷±œΏ…œΘ§ΝΫ÷±œΏΫΜΒψΒΡΚαΉχ±ξΈΣmΘ§«“ΒΎmΧλ»’œζ έΝΩΉν¥σ.
(Δώ)«σf(n) ΒΡ±μ¥ο ΫΘ§ΦΑ«ΑmΧλΒΡœζ έΉή ΐΘΜ
(Δρ)Α¥“‘ΆυΨ≠―ιΘ§Β±ΗΟΉ®¬τΒξœζ έΡ≥ΩνΖΰΉΑΒΡΉή ΐ≥§Ιΐ 400 Φΰ ±Θ§ –Οφ…œΜαΝς––ΗΟΩνΖΰΉΑΘ§Εχ»’œζ έΝΩΝ§–χœ¬ΫΒ≤ΔΒΆ”Ύ 30 Φΰ ±Θ§ΗΟΩνΖΰΉΑΫΪ≤Μ‘ΌΝς––. ‘‘Λ≤β±ΨΩνΖΰΉΑ‘Ύ –Οφ…œΝς––ΒΡΧλ ΐ «ΖώΜα≥§Ιΐ 10 ΧλΘΩ«κΥΒΟςάμ”….
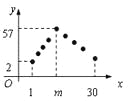
ΓΨ¥πΑΗΓΩ(Δώ)  Θ§Θ®n
Θ§Θ®n![]() N*Θ©Θ§354 ΦΰΘΜ(Δρ) ≤Μ≥§ΙΐΘ§άμ”…ΦϊΫβΈω.
N*Θ©Θ§354 ΦΰΘΜ(Δρ) ≤Μ≥§ΙΐΘ§άμ”…ΦϊΫβΈω.
ΓΨΫβΈωΓΩ
(I) ΗυΨίΧβ“βΘ§…η Θ§
Θ§
Εχf(1) = 2Θ§Γύ 5 +a= 2,a= Θ≠3Θ°
”÷ 5m+a= Θ≠3m+bΘ§Γύb= 8m+a= 8mΘ≠3Θ§
Γύ Θ°
Θ°
”…f(m) = 57ΒΟm= 12Θ°
![]()
«Α 12 ΧλΒΡœζ έΉήΝΩΈΣ 5 (1 + 2 + 3 + Γ≠ + 12)Θ≠3ΓΝ12 = 354ΦΰΘ°
(II) ΒΎ 13 ΧλΒΡœζ έΝΩΈΣf(13) = Θ≠3ΓΝ13 + 93 =" 54" ΦΰΘ§
Εχ 354 + 54 > 400 ΦΰΘ§
Γύ ¥”ΒΎ 14 ΧλΩΣ Φœζ έΉήΝΩ≥§Ιΐ 400 ΦΰΘ§Φ¥ΩΣ ΦΝς––Θ°
…ηΒΎx ΧλΒΡ»’œζ έΝΩΩΣ ΦΒΆ”Ύ 30 Φΰ (12 <xΓή 30)Θ§
Φ¥f(x) = Θ≠3x+ 93 < 30 Θ§
ΫβΒΟx> 21Θ°
¥”ΒΎ22ΧλΘ§»’œζ έΝΩΩΣ ΦΒΆ”Ύ 30 ΦΰΘ§21-13=8Θ§
ΓύΗΟΖΰΉΑΝς––ΒΡ ±Φδ≤Μ≥§Ιΐ10ΧλΘ°

ΓΨΧβΡΩΓΩœ÷Ε‘Ρ≥ –ΙΛ–ΫΫΉ≤ψΙΊ”ΎΓΑ¬Ξ –œόΙΚΝνΓ±ΒΡΧ§Ε»Ϋχ––Βς≤ι,ΥφΜζ≥ιΒςΝΥ50»Υ,ΥϊΟ«‘¬ ’»κΒΡΤΒ ΐΖ÷≤ΦΦΑΕ‘ΓΑ¬Ξ –œόΙΚΝνΓ±‘ό≥…»Υ ΐ»γ±μ:
‘¬ ’»κ(ΒΞΈΜΑΌ‘Σ) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
ΤΒ ΐ | 5 | 10 | 15 | 10 | 5 | 5 |
‘ό≥…»Υ ΐ | 4 | 8 | 12 | 5 | 2 | 1 |
(Δώ)”…“‘…œΆ≥ΦΤ ΐΨίΧνœ¬Οφ2ΓΝ2Ν–ΝΣ±μ≤ΔΈ «Ζώ”–99%ΒΡΑ―Έ’»œΈΣΓΑ‘¬ ’»κ“‘5500ΈΣΖ÷ΫγΒψΓ±Ε‘ΓΑ¬Ξ –œόΙΚΝνΓ±ΒΡΧ§Ε»”–≤ν“λ;
‘¬ ’»κΒΆ”Ύ55ΑΌ‘ΣΒΡ»Υ ΐ | ‘¬ ’»κ≤ΜΒΆ”Ύ55ΑΌ‘ΣΒΡ»Υ ΐ | ΚœΦΤ | |
‘ό≥… | |||
≤Μ‘ό≥… | |||
ΚœΦΤ |
(Δρ)»τ≤…”ΟΖ÷≤ψ≥ι―υ‘Ύ‘¬ ’»κ‘Ύ[15,25),[25,35)ΒΡ±ΜΒς≤ι»Υ÷–Ι≤ΥφΜζ≥ι»Γ6»ΥΫχ––ΉΖΉΌΒς≤ι,≤ΔΗχ”ηΤδ÷–3»ΥΓΑΚλΑϋΓ±Ϋ±άχ,«σ ’ΒΫΓΑΚλΑϋΓ±Ϋ±άχΒΡ3»Υ÷–÷Ν…Ό”–1»Υ ’»κ‘Ύ[15,25)ΒΡΗ≈¬ .
≤ΈΩΦΙΪ Ϋ:K2![]() ,Τδ÷–n=a+b+c+d.
,Τδ÷–n=a+b+c+d.
≤ΈΩΦ ΐΨί:
P(K2Γίk) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |