题目内容
(2005•朝阳区一模)有一个正四棱锥,它的底面边长与侧棱长均为a,现用一张正方形包装纸将其完全包住(不能裁剪纸,但可以折叠),那么包装纸的最小边长应为( )
分析:将四棱锥的四个侧面沿底面展开,观察展开图的形状形可得包装纸的对角线处在如图所示的P'P位置时,包装纸面积最小,由此结合正三角形和正方形的性质加以计算,即可获得问题的解答.
解答:解:由题意,得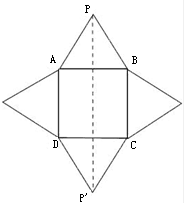
将正四棱锥沿底面将侧面都展开,得到如右图所示的平面展开图
可得当以P'P为正方形的对角线时所需正方形的包装纸的面积最小,
相应地,此时包装纸的边长也最小.
设包装纸正方形的边长为x,可得P'P2=2x2,
又∵P'P=a+2×
,∴P'P2=(a+
a)2=2x2,
解之得:x=
a
故选:B

将正四棱锥沿底面将侧面都展开,得到如右图所示的平面展开图
可得当以P'P为正方形的对角线时所需正方形的包装纸的面积最小,
相应地,此时包装纸的边长也最小.
设包装纸正方形的边长为x,可得P'P2=2x2,
又∵P'P=a+2×
| ||
| 2 |
| 3 |
解之得:x=
| ||||
| 2 |
故选:B
点评:本题给出正方形纸片将正四棱锥完全包住,求包装纸的最小边长考.着重考查了四棱锥的侧面展开图、正方形和正三角形的性质等知识,属于中档题.同时考查了图形的观察和分析能力、空间想象能力和空间问题平面化的思想,是一道值得同学们体会反思的好题.

练习册系列答案
相关题目
 (2005•朝阳区一模)设P(x,y)是图中四边形内的点或四边形边界上的点(即x、y满足的约束条件),则z=2x+y的最大值是
(2005•朝阳区一模)设P(x,y)是图中四边形内的点或四边形边界上的点(即x、y满足的约束条件),则z=2x+y的最大值是