题目内容
【题目】已知正方体
，点
是棱
的中点，设直线
为
，直线
为
.对于下列两个命题：①过点有且只有一条直线
与、都相交；②过点有且只有一条直线与、都成
角.以下判断正确的是（ ）
A.①为真命题，②为真命题B.①为真命题，②为假命题
C.①为假命题，②为真命题D.①为假命题，②为假命题
【答案】B
【解析】
作出过P与两直线相交的直线l判断①；通过平移直线a，b，结合异面直线所成角的概念判断②．
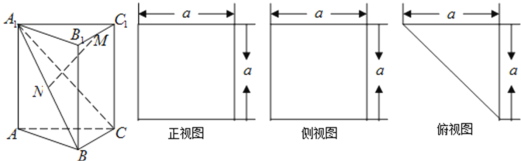
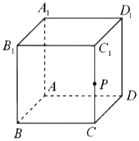
解：直线AB与A1D1 是两条互相垂直的异面直线，点P不在这两异面直线中的任何一条上，如图所示：
取BB1的中点Q，则PQ∥A1D1，且 PQ＝A1D1，设A1Q与AB交于E，则点A1、D1、Q、E、P共面，
直线EP必与A1D1 相交于某点F，则过P点有且只有一条直线EF与a、b都相交，故①为真命题；
分别平移a，b，使a与b均经过P，则有两条互相垂直的直线与a，b都成45°角，故②为假命题．
∴①为真命题，②为假命题．
故选：B．
练习册系列答案
相关题目
【题目】从某校随机抽取100名学生，获得了他们一周课外阅读时间（单位：小时）的数据，整理得到频数分布表和频率分布直方图如下．
组号 | 分组 | 频数 |
1 | [0，2） | 6 |
2 | [2，4） | 8 |
3 | [4，6） | 17 |
4 | [6，8） | 22 |
5 | [8，10） | 25 |
6 | [10，12） | 12 |
7 | [12，14） | 6 |
8 | [14，16） | 2 |
9 | [16，18） | 2 |
合计 | 100 |
（1）从该校随机选取一名学生，试估计这名学生该周课外阅读时间少于12小时的频率；
（2）求频率分布直方图中的a，b的值．
