题目内容

已知定义域为R的函数f(x)满足f(-x)=-f(x+6),且当x＞3时,f(x)单调递减,如果x1+x2＜6且(x1-3)(x2-3)＜0,则f(x1)+f(x2)的值

A.恒大于0                                 B.恒小于0

C.可能为0                                 D.可正可负

A?

解析:x换-x得f(x)=-f(6-x).?

令x=3得f(3)=-f(3),f(3)=0且f(x)关于(3,0)对称.?

又∵(x1-3)(x2-3)＜0,?

∴x1,x2中有一个比3大,一个比3小.?

又∵x1+x2＜6,?

∴x1,x2中(不妨设x1＜x2),?

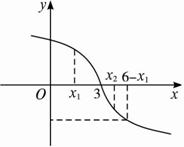
x1距3远,x2距3近.?

又∵x＞3时,f(x)＜0,?

∴f(x1)+f(x2)＞0恒成立.∴选A.?


练习册系列答案
相关题目
（2010•石家庄二模）已知定义域为R的函数f（x）在（1，+∞）上为减函数，且函数y=f（x+1）为偶函数，则（　　）
已知定义域为R的函数f（x）满足f（x）f（x+2）=5，若f（2）=3，则f（2012）=
5
3
5
3
．
已知定义域为R的函数f（x）在（4，+∞）上为减函数，且函数y=f（x）的对称轴为x=4，则（　　）
已知定义域为R的函数f(x)=
-2x+a2x+1
是奇函数
（1）求a值；
（2）判断并证明该函数在定义域R上的单调性；
（3）若对任意的t∈R，不等式f（t2-2t）+f（2t2-k）＜0恒成立，求实数k的取值范围；
（4）设关于x的函数F（x）=f（4x-b）+f（-2x+1）有零点，求实数b的取值范围．
已知定义域为R的函数f（x）满足f（4-x）=-f（x），当x＜2时，f（x）单调递减，如果x1+x2＞4且（x1-2）（x2-2）＜0，则f（x1）+f（x2）的值（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网