题目内容
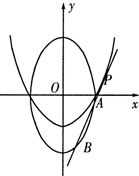 (2010•潍坊三模)如图,过抛物线C1:y=x2-1上一点P(不与顶点重合)的切 线l与曲线C2:x2+
(2010•潍坊三模)如图,过抛物线C1:y=x2-1上一点P(不与顶点重合)的切 线l与曲线C2:x2+| y2 | 4 |
(1)证明:弦AB的中点在一条定直线l0上;
(2)过P点且平行于(1)中直线l0的直线与曲线C1的另一交点为Q,与l平行的直线与曲线C1交于E、F两点,已知∠EQP=45°,试判断△EQF的形状,并说明理由.
分析:(1)设点P(t,t2-1),因为对曲线C1而言,所以l的斜率为y'|x=t=2t,直线l的方程为y=2tx-(t2+1).由
,得4(1+t2)x2-4t(1+t2)x+(1-t2)(3+t2)=0.再由根的判别式和韦达定理能够证明弦AB的中点在一条定直线l0:y=-1上.
(2)由P,Q两点关于y轴对称,知Q(-t,t2-1).设EF的方程为y=2tx+b,代入y=x2-1得x2-2tx-b-1=0.设E(xE,xE2-1),F(xF,xF2-1),则xE+xF=2t,因为kQF=
=xF-t,同理kQF=xE-t.所以kQF+kQE=(xE+xF)-2t=0.由此能够判断△EQF为直角三角形.
|
(2)由P,Q两点关于y轴对称,知Q(-t,t2-1).设EF的方程为y=2tx+b,代入y=x2-1得x2-2tx-b-1=0.设E(xE,xE2-1),F(xF,xF2-1),则xE+xF=2t,因为kQF=
(
| ||
| xF+t |
解答:解:(1)设点P(t,t2-1)
因为对曲线C1而言,所以l的斜率为y'|x=t=2t,
直线l的方程为y=2tx-(t2+1).
由
,
得4(1+t2)x2-4t(1+t2)x+(1-t2)(3+t2)=0.
由△=-16(1+t2)(t2-3)>0得-
<t<
.
设A(x1,y1),B(x2,y2),AB的中点为(x0,y0),
则x1+x2=t,y1+y2=2t(x1+x2)-2(t2+1)=-2,
从而y0=-1.
所以弦AB的中点在一条定直线l0:y=-1上.…(7分)
(2)由(1)知,P,Q两点关于y轴对称,所以Q(-t,t2-1).
设EF的方程为y=2tx+b,代入y=x2-1得x2-2tx-b-1=0.
设E(xE,xE2-1),F(xF,xF2-1),
则xE+xF=2t,因为kQF=
=xF-t,
同理kQF=xE-t.所以kQF+kQE=(xE+xF)-2t=0.
若点F在直线PQ下方,则直线PQ平分∠EQF.
因为∠EQP=
,所以∠EQF=
,
即△EQF为直角三角形;
若点F在直线PQ上方,设M为线段PQ左边延长线上一点,
则∠FQM=∠EQP=
,结论仍然成立.…(15分)
因为对曲线C1而言,所以l的斜率为y'|x=t=2t,
直线l的方程为y=2tx-(t2+1).
由
|
得4(1+t2)x2-4t(1+t2)x+(1-t2)(3+t2)=0.
由△=-16(1+t2)(t2-3)>0得-
| 3 |
| 3 |
设A(x1,y1),B(x2,y2),AB的中点为(x0,y0),
则x1+x2=t,y1+y2=2t(x1+x2)-2(t2+1)=-2,
从而y0=-1.
所以弦AB的中点在一条定直线l0:y=-1上.…(7分)
(2)由(1)知,P,Q两点关于y轴对称,所以Q(-t,t2-1).
设EF的方程为y=2tx+b,代入y=x2-1得x2-2tx-b-1=0.
设E(xE,xE2-1),F(xF,xF2-1),
则xE+xF=2t,因为kQF=
(
| ||
| xF+t |
同理kQF=xE-t.所以kQF+kQE=(xE+xF)-2t=0.
若点F在直线PQ下方,则直线PQ平分∠EQF.
因为∠EQP=
| π |
| 4 |
| π |
| 2 |
即△EQF为直角三角形;
若点F在直线PQ上方,设M为线段PQ左边延长线上一点,
则∠FQM=∠EQP=
| π |
| 4 |
点评:本题考查直线和圆锥曲线的位置关系,具有一定的难度,运算量大,解题繁琐,答题时要认真审题,合理地进行等价转化.

练习册系列答案
相关题目
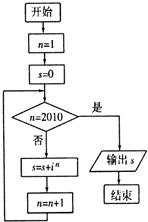 (2010•潍坊三模)运行如图所示的程序框图输出的结果是(其中i是虚数单位)( )
(2010•潍坊三模)运行如图所示的程序框图输出的结果是(其中i是虚数单位)( )