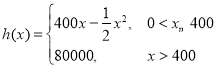[题目]把两个全等的正三棱锥的底面粘在一起.在所得的六面体中.所有二面角相等.而顶点可分成两类:在第一类中.每一个顶点发出三条棱,而在第二类顶点中.每一个顶点发出四条棱.试求连结两个第一类顶点的线段长与连结两个第二类顶点的线段长之比. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】把两个全等的正三棱锥的底面粘在一起，在所得的六面体中，所有二面角相等，而顶点可分成两类：在第一类中，每一个顶点发出三条棱；而在第二类顶点中，每一个顶点发出四条棱。试求连结两个第一类顶点的线段长与连结两个第二类顶点的线段长之比。

【答案】

【解析】

设D-ABC和E-ABC是全等的正三棱锥，它们的底面是正.

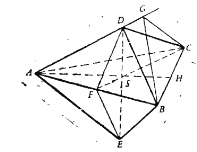
如果将它们的底面粘在一起，那么所得的六面体的顶点D和E应该通过的重心，且在与平面ABC垂直的直线上，这样所得的六面体不仅关于平面ABC对称，而且关于平面ADE对称.

由对称性推出由顶点D，E作棱AB的垂线段相等，设F为垂足，则是二面角D-AB-E的平面角.

同样，由顶点B，C作棱AD的垂线段也相等，设G为垂足，则是二面角B-AD-C的平面角.

由题设可证明也是等边三角形，其边长的比等于它们的高之比.即

.而，有.

练习册系列答案

(1)若从这6个国家中任选2个，求这2个国家都是亚洲国家的概率；

(2)若从亚洲国家和欧洲国家中各选1个，求这两个国家包括A1，但不包括B1的概率．

【题目】如图，过抛物线上一点P（1，-2）作倾斜角互补的两条直线，分别与抛物线交于点.

（1）求的值；

（2）若，求面积的最大值。

【题目】2018年8月31日，十三届全国人大常委会第五次会议表决通过了关于修改个人所得税法的决定，这是我国个人所得税法自1980年出台以来第七次大修为了让纳税人尽早享受减税红利，在过渡期对纳税个人按照下表计算个人所得税，值得注意的是起征点变为5000元，即如表中“全月应纳税所得额”是纳税者的月薪金收入减去5000元后的余额．

级数	全月应纳税所得额	税率
1	不超过3000元的部分
2	超过3000元至12000元的部分
3	超过12000元至25000元的部分

某企业员工今年10月份的月工资为15000元，则应缴纳的个人所得税为______元

【题目】共享单车是城市慢行系统的一种创新模式，对于解决民众出行“最后一公里”的问题特别见效，由于停取方便、租用价格低廉，各色共享单车受到人们的热捧．某自行车厂为共享单车公司生产新样式的单车，已知生产新样式单车的固定成本为20 000元，每生产一辆新样式单车需要增加投入100元．根据初步测算，自行车厂的总收益(单位：元)满足分段函数其中x是新样式单车的月产量(单位：辆)，利润＝总收益－总成本．

(1)试将自行车厂的利润y元表示为月产量x的函数；

(2)当月产量为多少件时自行车厂的利润最大？最大利润是多少？

【题目】为响应绿色出行，前段时间大连市在推出“共享单车”后，又推出“新能源分时租赁汽车”，其中一款新能源分时租赁汽车，每次租车收费的标准由两部分组成：①根据行驶里程按1元/公里计费；②行驶时间不超过40分钟时，按0.12元/分钟计费：超出部分按0.20元/分钟计费，己知张先生家离上班地点15公里，每天租用该款汽车上、下班各一次.由于堵车、红路灯等因素，每次路上开车花费的时间（分钟）是一个随机变量.现统计了100次路上开车花费时间，在各时间段内的频数分布情况如下表所示：