题目内容
10.已知数列{an}的前n项和Sn=-n2+2n+1.(1)求{an}的通项公式;
(2)若等差数列{an}的前n项和Sn=An2+Bn+C(A,B,C为常数),则常数A,B,C必满足何条件?
分析 (1)利用“当n=1时,a1=S1;当n≥2时,an=Sn-Sn-1”即可得出.
(2)根据当n≥2时,an=Sn-Sn-1”求出数列的通项公式,结合等差数列的定义进行判断即可.
解答 解:(1)当n≥2时,an=Sn-Sn-1=-n2+2n-1-[-(n-1)2+2(n-1)-1]=-2n+3,
当n=1时,a1=S1=-1+2+1=2,不适合上式,
∴数列{an}的通项公式an=$\left\{\begin{array}{l}{2,}&{n=1}\\{-2n+3,}&{n≥2}\end{array}\right.$.
(2)当n≥2时,an=Sn-Sn-1=(An2+Bn+C)-[A(n-1)2+B(n-1)+C]
=(Aa2+Bn)-(An2-2An+A+Bn-B)=2An-A+B.
当n=1时,a1=S1=A+B+C,
则当C=0时,a1满足an=2An-A+B,此时数列{an}为等差数列.公差d-2A,
当C≠0时,a1不满足an=2An-A+B,此时数列{an}不为等差数列.
点评 本题考查数列{an}的通项公式与前n项和为Sn的关系式,熟练掌握“当n=1时,a1=S1;当n≥2时,an=Sn-Sn-1”是解题的关键,注意验证n=1时是否适合.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.下列推理中属于归纳推理且结论正确的是( )
| A. | 设数列﹛an﹜的前n项和为sn,由an=2n-1,求出s1=12,s2=22,s3=32,…推断sn=n2 | |
| B. | 由f(x)=xcosx,满足f(-x)=-f(x)对?x∈R都成立,推断f(x)=xcosx为奇函数 | |
| C. | 由圆x2+y2=r2的面积s=πr2推断:椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的面积s=πab | |
| D. | 由(1+1)2>21,(2+1)2>22,(3+1)2>23,…,推断对一切正整数n,(n+1)2>2n |
18.在△ABC中,已知AC=$\sqrt{19}$,BC=2,B=$\frac{2π}{3}$,则边AC上的高为( )
| A. | $\frac{3\sqrt{19}}{19}$ | B. | $\frac{3\sqrt{57}}{19}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
15.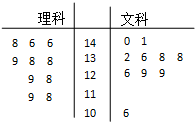 某校在一次期中考试结束后,把全校文、理科总分前10名学生的数学成绩(满分150分)抽出来进行对比分析,得到如图所示的茎叶图.若从数学成绩高于120分的学生中抽取3人,分别到三个班级进行数学学习方法交流,则满足理科人数多于文科人数的情况有( )种.
某校在一次期中考试结束后,把全校文、理科总分前10名学生的数学成绩(满分150分)抽出来进行对比分析,得到如图所示的茎叶图.若从数学成绩高于120分的学生中抽取3人,分别到三个班级进行数学学习方法交流,则满足理科人数多于文科人数的情况有( )种.
 某校在一次期中考试结束后,把全校文、理科总分前10名学生的数学成绩(满分150分)抽出来进行对比分析,得到如图所示的茎叶图.若从数学成绩高于120分的学生中抽取3人,分别到三个班级进行数学学习方法交流,则满足理科人数多于文科人数的情况有( )种.
某校在一次期中考试结束后,把全校文、理科总分前10名学生的数学成绩(满分150分)抽出来进行对比分析,得到如图所示的茎叶图.若从数学成绩高于120分的学生中抽取3人,分别到三个班级进行数学学习方法交流,则满足理科人数多于文科人数的情况有( )种.| A. | 3081 | B. | 1512 | C. | 1848 | D. | 2014 |
20.已知A(-1,0),B(5,6),C(3,4),则$\frac{{|{CB}|}}{{|{AC}|}}$=( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 3 | D. | 2 |