题目内容
若实数x,y满足 则x2-2xy+y2的取值范围是( )
则x2-2xy+y2的取值范围是( )
 则x2-2xy+y2的取值范围是( )
则x2-2xy+y2的取值范围是( )| A.[0,4] | B.[0, ] ] |
C.[4, ] ] | D.[0, ] ] |
B
将x2-2xy+y2变形为(x-y)2,只需求出x-y的取值范围即可得到(x-y)2的取值范围.
画出可行域(如图),

x2-2xy+y2=(x-y)2,令z=x-y,则y=x-z,可知当直线y=x-z经过点M(- ,3)时z取最小值zmin=-
,3)时z取最小值zmin=- ;当直线y=x-z经过点P(5,3)时z取最大值zmax=2,即-
;当直线y=x-z经过点P(5,3)时z取最大值zmax=2,即- ≤z=x-y≤2,所以0≤x2-2xy+y2≤
≤z=x-y≤2,所以0≤x2-2xy+y2≤ .
.
画出可行域(如图),

x2-2xy+y2=(x-y)2,令z=x-y,则y=x-z,可知当直线y=x-z经过点M(-
 ,3)时z取最小值zmin=-
,3)时z取最小值zmin=- ;当直线y=x-z经过点P(5,3)时z取最大值zmax=2,即-
;当直线y=x-z经过点P(5,3)时z取最大值zmax=2,即- ≤z=x-y≤2,所以0≤x2-2xy+y2≤
≤z=x-y≤2,所以0≤x2-2xy+y2≤ .
.
练习册系列答案
相关题目
 分别在直线
分别在直线 的两侧,则
的两侧,则 的取值范围是
的取值范围是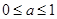

 或
或
 或
或
 求z的最大值和最小值.
求z的最大值和最小值. 所表示的平面区域被直线y=kx+2分为面积相等的两部分,则k的值为( )
所表示的平面区域被直线y=kx+2分为面积相等的两部分,则k的值为( )


 ,且目标函数z=2x+y的最大值是最小值的8倍,则实数a的值是( )
,且目标函数z=2x+y的最大值是最小值的8倍,则实数a的值是( )



 则z=
则z=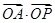 的最大值为( )
的最大值为( ) 目标函数z=x+2y最大值记为a,最小值记为b,则a-b的值为________.
目标函数z=x+2y最大值记为a,最小值记为b,则a-b的值为________.