题目内容
【题目】请你帮忙设计2010年玉树地震灾区小学的新校舍，如图，在学校的东北力有一块地，其中两面是不能动的围墙，在边界
内是不能动的一些体育设施．现准备在此建一栋教学楼，使楼的底面为一矩形，且靠围墙的方向须留有5米宽的空地，问如何设计，才能使教学楼的面积最大？
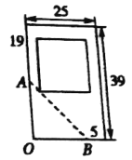
【答案】在线段
上取点
，过点分别作墙的平行线，建一个长、宽都为17米的正方形，教学楼的面积最大
【解析】
可建立如图所示的平面直角坐标系，根据截距式写出AB所在直线方程
，
然后可设G点的坐标为
，再根据题目中的要求可列出教学楼的面积的表达式
,
,然后利用一元二次函数求最值即可。
解：如图建立坐标系，
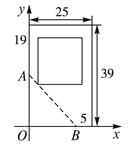
可知所在直线方程为
，即.
设
，由
可知
．
∴
.
由此可知，当
时，
有最大值289平方米．
故在线段上取点
，过点分别作墙的平行线，建一个长、宽都为17米的正方形，教学楼的面积最大．
练习册系列答案
相关题目
【题目】某种农作物可以生长在滩涂和盐碱地，它的灌溉是将海水稀释后进行灌溉.某实验基地为了研究海水浓度
对亩产量
(吨)的影响,通过在试验田的种植实验,测得了该农作物的亩产量与海水浓度的数据如下表：
海水浓度 |
|
|
|
|
|
亩产量 |
|
|
|
|
|
残差 |
|
|
|
|
|
绘制散点图发现,可以用线性回归模型拟合亩产量(吨)与海水浓度之间的相关关系，用最小二乘法计算得与
之间的线性回归方程为
.
（1）求
的值；
（2）统计学中常用相关指数
来刻画回归效果，越大，回归效果越好，如假设
，就说明预报变量的差异有
是解释变量引起的.请计算相关指数(精确到
),并指出亩产量的变化多大程度上是由浇灌海水浓度引起的？
（附：残差
，相关指数
，其中
）
