题目内容
已知双曲线方程为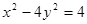 , 则以M(4,1)为中点的弦所在直线l的方程是 .
, 则以M(4,1)为中点的弦所在直线l的方程是 .
x-y-3=0
解析试题分析:因为双曲线方程为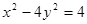 ,设弦端点的坐标为A(m,n),B(s,t)
,设弦端点的坐标为A(m,n),B(s,t)
那么将两点代入方程中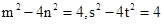 作差得到(m+s(m-s)-4(n-t)(n+t))=0
作差得到(m+s(m-s)-4(n-t)(n+t))=0
由中点公式可知为(4,1)m+s=8,n+t=2,可知直线的斜率为1,故由点斜式方程得到,直线方程为x-y-3=0,答案为x-y-3=0。
考点:本题主要考查了双曲线的应用,圆锥曲线与直线的关系,弦长公式等.考查了学生综合分析和推理的能力.
点评:解决该试题的关键是设出直线AB的方程与双曲线方程联立消去y,设两实根为x1,x2,利用韦达定理可表示出x1+x2的值,根据P点坐标求得x1+x2=4进而求得k,则直线AB的方程可得,进而利用弦长公式求得|AB|.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
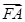 +
+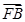 +
+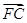 =0,则|
=0,则|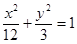 的左焦点为
的左焦点为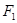 , 点
, 点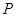 在椭圆上, 如果线段
在椭圆上, 如果线段 的中点
的中点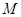 在
在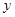 轴的
轴的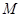 的坐标是 .
的坐标是 . 与双曲线
与双曲线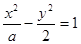 有相同的焦点,则实数
有相同的焦点,则实数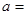 _________。
_________。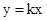 是曲线
是曲线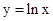 的切线,则
的切线,则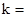 。
。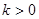 ,则方程
,则方程 有实根;
有实根;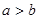 ,则
,则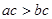 ”的否命题;
”的否命题;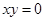 ,则
,则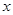 、
、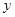 至少有一个为零”的逆否命题 .
至少有一个为零”的逆否命题 .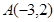 的抛物线的标准方程是
的抛物线的标准方程是 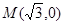 ,椭圆
,椭圆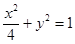 与直线
与直线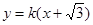 交于点
交于点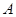 、
、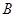 ,则
,则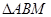 的周长为 .
的周长为 .