题目内容
已知直线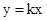
是曲线
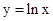的切线，则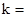
。
．
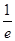
解析试题分析：设切点坐标为（m，n）,y'|x=m=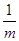
=k,解得，m=
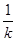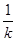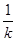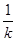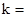
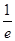,n=km,切点（，n）在曲线y=lnx的图象上,∴n=-lnk，,而切点（，n）又在直线y=kx上,∴,n="1," =e,,故填写．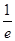
考点：本题主要考查了利用导数研究曲线上某点切线方程，考查运算求解能力，考查数形结合思想、化归与转化思想，属于基础题．
点评：解决该试题的关键是先设出切点坐标，根据导数的几何意义求出在切点处的导数，从而求出切点横坐标，再根据切点既在曲线y=lnx的图象上又在直线y=kx上，即可求出k的值
练习册系列答案
名校课堂系列答案
相关题目
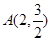，点
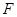是抛物线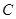
：
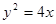的焦点，点
是抛物线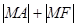
取最小值时点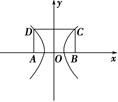
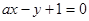经过抛物线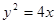
的焦点,则实数
= 
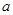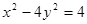, 则以M(4,1)为中点的弦所在直线l的方程是 . 
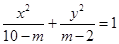，若其长轴在
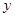轴上.焦距为
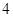，则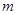
等于___________。
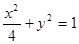的两个焦点分别为
，过
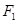作垂直于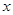
轴的直线与椭圆相交，其中一个交点为
，则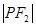
= .
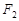为圆心作一个圆，使此圆过椭圆中心并交椭圆于点M，N，
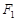的直线MF1是圆