题目内容
设F为抛物线y2=4x的焦点,A、B、C为该抛物线上三点,若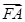 +
+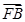 +
+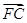 =0,则|
=0,则|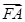 |+|
|+|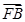 |+|
|+|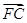 |=___________。
|=___________。
6
解析试题分析:设A(x1,y1),B(x2,y2),C(x3,y3),抛物线焦点坐标F(1,0),准线方程:x=-1,因为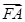 +
+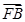 +
+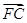 =0,所以点F是△ABC重心,则x1+x2+x2=3, y,+y2+y3=0,而|FA|=x1-(-1)=x1+1, |FB|=x2-(-1)=x2+1, |FC|=x3-(-1)=x3+1,所以|FA|+|FB|+|FC|= x1+1+ x2+1+ x3+1="(" x1+ x2+ x3)+3=3+3=6。
=0,所以点F是△ABC重心,则x1+x2+x2=3, y,+y2+y3=0,而|FA|=x1-(-1)=x1+1, |FB|=x2-(-1)=x2+1, |FC|=x3-(-1)=x3+1,所以|FA|+|FB|+|FC|= x1+1+ x2+1+ x3+1="(" x1+ x2+ x3)+3=3+3=6。
考点:抛物线的简单性质;重心的性质;重心的坐标公式。
点评:在∆ABC中,设A(x1,y1),B(x2,y2),C(x3,y3),则∆ABC重心的坐标为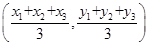 。
。

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目
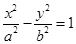 的一条渐近线方程为
的一条渐近线方程为 ,则其离心率为 。
,则其离心率为 。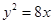 ,焦点为
,焦点为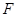 ,准线为
,准线为 ,
,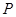 为抛物线上一点,
为抛物线上一点,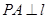 ,
, 为垂足,如果直线
为垂足,如果直线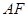 的斜率为
的斜率为 ,那么
,那么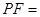 。
。 过点
过点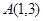 , 且直线
, 且直线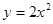 交于
交于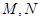 两点. 若
两点. 若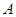 点恰好是
点恰好是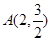 ,点
,点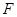 是抛物线
是抛物线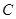 :
: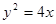 的焦点,点
的焦点,点 是抛物线
是抛物线 取最小值时点
取最小值时点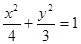 的左、右焦点分别为F1、F2,过椭圆的右焦点F2作一条直线l交椭圆与P、Q两点,则△F1PQ内切圆面积的最大值是
的左、右焦点分别为F1、F2,过椭圆的右焦点F2作一条直线l交椭圆与P、Q两点,则△F1PQ内切圆面积的最大值是  ,
,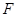 为其焦点,
为其焦点, 为抛物线上的任意点,则线段
为抛物线上的任意点,则线段 中点的轨迹方程是 .
中点的轨迹方程是 .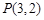 且与双曲线
且与双曲线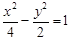 有相同渐近线方程的双曲线的标准方程为 .
有相同渐近线方程的双曲线的标准方程为 .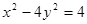 , 则以M(4,1)为中点的弦所在直线l的方程是 .
, 则以M(4,1)为中点的弦所在直线l的方程是 .