题目内容
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,点E,F分别在
,点E,F分别在![]() ,
,![]() ,且
,且![]() ,
,![]() .设
.设![]() .
.

(1)当![]() 时,求异面直线
时,求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(2)当平面![]() 平面
平面![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)60°(2)![]()
【解析】
(1)推导出![]() 平面ABC,
平面ABC,![]() AC,建立分别以AB,AC,
AC,建立分别以AB,AC,![]() 为
为![]() 轴的空间直角坐标系,利用法向量能求出异面直线AE与
轴的空间直角坐标系,利用法向量能求出异面直线AE与![]() 所成角.
所成角.
(2)推导出平面![]() 的法向量和平面
的法向量和平面![]() 的一个法向量,由平面
的一个法向量,由平面![]() 平面
平面![]() ,能求出
,能求出![]() 的值.
的值.
解:因为直三棱柱![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
,
所以![]() ,
,![]() ,
,
又因为![]() ,
,
所以建立分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴的空间直角坐标系
轴的空间直角坐标系![]() .
.

(1)设![]() ,则
,则![]() ,
,![]() ,
,
各点的坐标为![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() .
.
因为![]() ,
,![]() ,
,
所以 .
.
所以向量![]() 和
和![]() 所成的角为120°,
所成的角为120°,
所以异面直线![]() 与
与![]() 所成角为60°;
所成角为60°;
(2)因为![]() ,
,![]() ,
,
![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]() ,
,
则![]() ,且
,且![]() .
.
即![]() ,且
,且![]() .
.
令![]() ,则
,则![]() ,
,![]() .
.
所以![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
同理,![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
因为平面![]() 平面
平面![]() ,
,
所以![]() ,
,
![]() ,
,
解得![]() .
.
所以当平面![]() 平面
平面![]() 时,
时,![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】在某次测验中,某班40名考生的成绩满分100分统计如图所示.
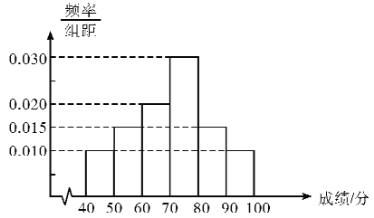
(Ⅰ)估计这40名学生的测验成绩的中位数![]() 精确到0.1;
精确到0.1;
(Ⅱ)记80分以上为优秀,80分及以下为合格,结合频率分布直方图完成下表,并判断是否有95%的把握认为数学测验成绩与性别有关?
合格 | 优秀 | 合计 | |
男生 | 16 | ||
女生 | 4 | ||
合计 | 40 |
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]()