题目内容
9.已知中心在原点,对称轴为坐标轴的椭圆,左焦点F1(-1,0),一个顶点坐标为(0,1).(1)求椭圆方程;
(2)直线l过椭圆的右焦点F2交椭圆于A、B两点,当△AOB面积最大时,求直线l方程.
分析 (1)由题意可设椭圆的标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),由c=1,b=1,a2=b2+c2,即可得出.
(2)设直线l的方程为my=x-1,A(x1,y1),B(x2,y2).与椭圆方程联立可得:(2+m2)y2+2my-1=0,利用根与系数的关系可得:|AB|=$\sqrt{(1+{m}^{2})[({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}]}$,利用点到直线的距离公式可得:原点O到直线l的距离d.利用S△AOB=$\frac{1}{2}d|AB|$,及其基本不等式的性质即可得出.
解答 解:(1)由题意可设椭圆的标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),
又c=1,b=1,∴a2=b2+c2=2.
∴椭圆的标准方程为:$\frac{{x}^{2}}{2}+{y}^{2}$=1.
(2)F2(1,0),
设直线l的方程为my=x-1,A(x1,y1),B(x2,y2).
联立$\left\{\begin{array}{l}{my=x-1}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,化为(2+m2)y2+2my-1=0,
∴y1+y2=-$\frac{2m}{2+{m}^{2}}$,y1y2=$\frac{-1}{2+{m}^{2}}$.
∴|AB|=$\sqrt{(1+{m}^{2})[({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}]}$=$\sqrt{(1+{m}^{2})[(\frac{-2m}{2+{m}^{2}})^{2}-4×\frac{-1}{2+{m}^{2}}]}$=$\frac{2\sqrt{2}(1+{m}^{2})}{2+{m}^{2}}$.
原点O到直线l的距离d=$\frac{1}{\sqrt{1+{m}^{2}}}$.
∴S△AOB=$\frac{1}{2}d|AB|$=$\frac{\sqrt{2}\sqrt{1+{m}^{2}}}{2+{m}^{2}}$=$\frac{\sqrt{2}}{\frac{1}{\sqrt{1+{m}^{2}}}+\sqrt{1+{m}^{2}}}$$≤\frac{\sqrt{2}}{2}$,当且仅当m=0时取等号.
此时直线l的方程为:x=1.
因此当△AOB面积最大为$\frac{\sqrt{2}}{2}$时,直线l方程为x=1.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交弦长问题、一元二次方程的根与系数的关系、点到直线的距离公式、三角形面积计算公式、基本不等式的性质,考查了推理能力与计算能力,属于难题.

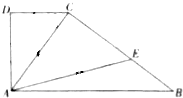 如图所示直角梯形ABCD中,∠BAD=∠ADC=90°,∠ACD=60°,AB=3DC=3,若线段BC上存在点E,使得AC、AE、AB成等比数列,则$\frac{CE}{CB}$等于( )
如图所示直角梯形ABCD中,∠BAD=∠ADC=90°,∠ACD=60°,AB=3DC=3,若线段BC上存在点E,使得AC、AE、AB成等比数列,则$\frac{CE}{CB}$等于( )| A. | $\frac{1+\sqrt{15}}{7}$ | B. | $\frac{6-\sqrt{15}}{7}$ | C. | $\frac{\sqrt{87}-9}{7}$ | D. | $\frac{18-\sqrt{87}}{7}$ |
| A. | (0,1) | B. | (1,1) | C. | (1,-1) | D. | (1,0) |
| A. | 最大值是f(1),最小值是f(3) | B. | 最大值是f(3),最小值是f(1) | ||
| C. | 最大值是f(1),最小值是f(2) | D. | 最大值是f(2),最小值是f(3) |