题目内容
【题目】已知函数 ![]() 存在互不相等实数a,b,c,d,有f(a)=f(b)=f(c)=f(d)=m.现给出三个结论:
存在互不相等实数a,b,c,d,有f(a)=f(b)=f(c)=f(d)=m.现给出三个结论:
⑴m∈[1,2);
⑵a+b+c+d∈[e﹣3+e﹣1﹣2,e﹣4﹣1),其中e为自然对数的底数;
⑶关于x的方程f(x)=x+m恰有三个不等实根.
正确结论的个数为( )
A.0个
B.1个
C.2个
D.3个
【答案】C
【解析】解:作出函数 ![]() 的图象如图,
的图象如图,
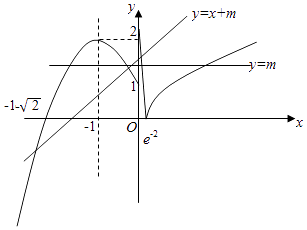
若直线y=m与函数y=f(x)的图象相交于四个不同的点,由图可知m∈[1,2),
故(1)正确;
设y=m与函数y=f(x)的交点自左至右依次为a,b,c,d,
由﹣2﹣lnx=1,得x=e﹣3,由﹣2﹣lnx=2,得x=e﹣4,
∴c∈(e﹣4,e﹣3],
又﹣2﹣lnc=2+lnd,∴cd=e﹣4,
∴a+b+c+d=﹣2+c+ ![]() 在(e﹣4,e﹣3]上是递减函数,
在(e﹣4,e﹣3]上是递减函数,
∴a+b+c+d∈[e﹣3+e﹣1﹣2,e﹣4﹣1),
故(2)正确;
设斜率为1的直线与y=lnx+2相切于(x0,lnx0+2),
则由 ![]() ,可得x0=1,则切点为(1,2),
,可得x0=1,则切点为(1,2),
此时直线方程为y﹣2=1×(x﹣1),即y=x+1,
∴当m=1时,直线y=x+m与函数y=f(x)有4个不同交点,即关于x的方程f(x)=x+m有四个不等实根,
故(3)错误.
∴正确结论的个数是2个.
故选:C.
作出分段函数的图象,根据数形结合,逐个分析可得出(1)(2)为正确结论.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目