题目内容
 (2011•潍坊二模)如图,在七面体ABCDMN中,四边形ABCD是边长为2的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=2,NB=1,MB与ND交于P点,点Q在AB上,且BQ=
(2011•潍坊二模)如图,在七面体ABCDMN中,四边形ABCD是边长为2的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=2,NB=1,MB与ND交于P点,点Q在AB上,且BQ=| 2 | 3 |
(I)求证:QP∥平面AMD;
(Ⅱ)求七面体ABCDMN的体积.
分析:(I)由MD⊥平面ABCD,NB⊥平面ABCD,利用线面垂直的性质可得MD∥NB.进而得到
=
=
,又已知
=
=
,可得
=
,于是在△MAB中,QP∥AM.再利用线面平行的性质即可得出QP∥平面AMD.
(II)连接BD,AC交于点O,则AC⊥BD.又MD⊥平面ABCD,利用线面垂直的性质可得MD⊥AC,再利用线面垂直的判定即可得出AC⊥平面MNBD.于是AO为四棱锥A-MNBD的高,进而得到VA-MNBD的体积.即可得出V几何体ABCDMN=2VA-MNBD.
| BP |
| PM |
| NB |
| MD |
| 1 |
| 2 |
| QB |
| QA |
| ||
2-
|
| 1 |
| 2 |
| QB |
| QA |
| BP |
| PM |
(II)连接BD,AC交于点O,则AC⊥BD.又MD⊥平面ABCD,利用线面垂直的性质可得MD⊥AC,再利用线面垂直的判定即可得出AC⊥平面MNBD.于是AO为四棱锥A-MNBD的高,进而得到VA-MNBD的体积.即可得出V几何体ABCDMN=2VA-MNBD.
解答:(I)证明:∵MD⊥平面ABCD,NB⊥平面ABCD,
∴MD∥NB.
∴
=
=
,又
=
=
,
∴
=
,
∴在△MAB中,QP∥AM.
又QP?平面AMD,AM?平面AMD.
∴QP∥平面AMD.
(II)连接BD,AC交于点O,则AC⊥BD.
又MD⊥平面ABCD,∴MD⊥AC,又BD∩MD=D,
∴AC⊥平面MNBD.
∴AO为四棱锥A-MNBD的高,又SMNBD=
×(1+2)×2
=3
.
∴VA-MNBD=
×3
×
=2.
∴V几何体ABCDMN=2VA-MNBD=4.
∴MD∥NB.
∴
| BP |
| PM |
| NB |
| MD |
| 1 |
| 2 |
| QB |
| QA |
| ||
2-
|
| 1 |
| 2 |
∴
| QB |
| QA |
| BP |
| PM |
∴在△MAB中,QP∥AM.
又QP?平面AMD,AM?平面AMD.
∴QP∥平面AMD.
(II)连接BD,AC交于点O,则AC⊥BD.
又MD⊥平面ABCD,∴MD⊥AC,又BD∩MD=D,
∴AC⊥平面MNBD.
∴AO为四棱锥A-MNBD的高,又SMNBD=
| 1 |
| 2 |
| 2 |
| 2 |
∴VA-MNBD=
| 1 |
| 3 |
| 2 |
| 2 |
∴V几何体ABCDMN=2VA-MNBD=4.
点评:熟练掌握线面平行于垂直的判定与性质、线线平行的判定与性质、四棱锥的体积等是解题的关键.

练习册系列答案
相关题目
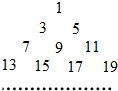 (2011•潍坊二模)已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是
(2011•潍坊二模)已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是 (2011•潍坊二模)运行如图的程序框图,当输入m=-4时的输出结果为n,若变量x,y满足
(2011•潍坊二模)运行如图的程序框图,当输入m=-4时的输出结果为n,若变量x,y满足