Question

6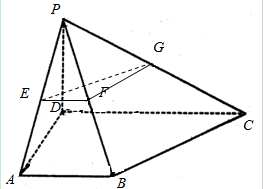．如图，在四棱锥P-ABCD的底面为直角梯形，且∠BAD=∠ADC=90°，E，F，G分别为PA，PB，PC的中点，直线PB⊥平面EFG，AB=$\frac{1}{3}$DC=$\frac{1}{3}$AD=1．
（1）若点M∈平面EFG，且与点E不重合，判断直线EM与平面ABCD的关系，并说明理由；
（2）若直线PD与平面PBC的夹角为30°，求四棱锥P-ABCD的体积．

Answer 1

分析 （1）利用三角形中位线的性质结合面面平行的判定定理得到面EFG∥面ABCD，然后可得直线EM∥平面ABCD；
（2）找出直线PD与平面PBC的夹角，通过解直角三角形求得四棱锥P-ABCD的高，然后直接代入棱锥的体积得答案．

解答 解：（1）如图，直线EM∥平面ABCD．
事实上：
∵E，F，G分别为PA，PB，PC的中点，
∴EF∥AB，FG∥BC，
∴平面EFG∥平面ABC，
∵点M∈平面EFG，且与点E不重合，∴直线EM∥平面ABCD；
（2）∵直线PB⊥平面EFG，∴面PBC⊥面ABCD，
又面PBC∩面ABCD=BC，
在面ABCD内过D作DN⊥BC，垂足为N，连接PN，则∠DPN为直线PD与平面PBC的夹角为30°，
在直角梯形ABCD中，由AB=$\frac{1}{3}$DC=$\frac{1}{3}$AD=1，得sin$∠BCD=\frac{3\sqrt{13}}{13}$，cos$∠BCD=\frac{2\sqrt{13}}{13}$，
∴$CN=DC•cos∠BCD=3×\frac{2\sqrt{13}}{13}=\frac{6\sqrt{13}}{13}$，$BN=\sqrt{13}-\frac{6\sqrt{13}}{13}=\frac{7\sqrt{13}}{13}$，
DN=DC$•sin∠BCD=3×\frac{3\sqrt{13}}{3}=\frac{9\sqrt{13}}{13}$，
∴$PN=\frac{DN}{tan30°}=\frac{\frac{9\sqrt{13}}{13}}{\frac{\sqrt{3}}{3}}=\frac{9\sqrt{39}}{13}$，
∴$PB=\sqrt{P{N}^{2}-B{N}^{2}}$=$\sqrt{（\frac{9\sqrt{39}}{13}）^{2}-（\frac{7\sqrt{13}}{13}）^{2}}$=$\frac{2\sqrt{753}}{13}$．
${S}_{梯形ABCD}=\frac{1}{2}×3（1+3）=6$，
∴${V}_{P-ABCD}=\frac{1}{3}×6×\frac{2\sqrt{753}}{13}=\frac{4\sqrt{753}}{13}$．

点评 本小题主要考查空间线面关系、二面角的度量、几何体的体积等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力，是中档题．