题目内容
14.在数列{an}中,a1=1,a2=3,且满足$\frac{{a}_{n+2}}{n+2}$=$\frac{{a}_{n}}{n}$+$\frac{3}{{2}^{n+1}}$.(1)记bn=$\frac{{a}_{n}}{n}$,求{bn}的通项公式;
(2)求数列{an}的前n项和Sn;
(3)证明不等式Sn-n(n+1)≤-1,n∈N*.
分析 (1)根据题目给出的数列递推式,分n为奇数和偶数利用累积法求得数列的通项公式;
(2)由(1)中数列{bn}的通项公式求数列{an}的通项公式,然后利用错位相减法求得数列{an}的前n项和Sn;
(3)由Sn-n(n+1)=$\frac{n+2}{{2}^{n-1}}-4$,然后利用数学归纳法证明数列不等式$\frac{n+2}{{2}^{n-1}}-4≤-1$.
解答 (1)解:由$\frac{{a}_{n+2}}{n+2}$=$\frac{{a}_{n}}{n}$+$\frac{3}{{2}^{n+1}}$,得
当n为奇数时,
$\frac{{a}_{3}}{3}=\frac{{a}_{1}}{1}+\frac{3}{{2}^{2}}$,
$\frac{{a}_{5}}{5}=\frac{{a}_{3}}{3}+\frac{3}{{2}^{4}}$,
…
$\frac{{a}_{n}}{n}=\frac{{a}_{n-2}}{n-2}+\frac{3}{{2}^{n-1}}$,
累加得:$\frac{{a}_{n}}{n}=\frac{{a}_{1}}{1}+3(\frac{1}{{2}^{2}}+\frac{1}{{2}^{4}}+…+\frac{1}{{2}^{n-1}})$
=$1+3•\frac{\frac{1}{4}(1-\frac{1}{{4}^{\frac{n-1}{2}}})}{1-\frac{1}{4}}$=$2-\frac{1}{{2}^{n-1}}$,
∴${b}_{n}=2-\frac{1}{{2}^{n-1}}$;
当n为偶数时,
$\frac{{a}_{4}}{4}=\frac{{a}_{2}}{2}+\frac{3}{{2}^{3}}$,
$\frac{{a}_{6}}{6}=\frac{{a}_{4}}{4}+\frac{3}{{2}^{5}}$,
…
$\frac{{a}_{n}}{n}=\frac{{a}_{n-2}}{n-2}+\frac{3}{{2}^{n-1}}$,
累加得:$\frac{{a}_{n}}{n}=\frac{{a}_{2}}{2}+3(\frac{1}{{2}^{3}}+\frac{1}{{2}^{5}}+…+\frac{1}{{2}^{n-1}})$
=$\frac{3}{2}+3•\frac{\frac{1}{8}(1-\frac{1}{{2}^{\frac{n-2}{2}}})}{1-\frac{1}{4}}$=$2-\frac{1}{{2}^{n-1}}$,
∴${b}_{n}=2-\frac{1}{{2}^{n-1}}$.
综上,${b}_{n}=2-\frac{1}{{2}^{n-1}}$(n∈N*);
(2)解:由${b}_{n}=2-\frac{1}{{2}^{n-1}}$,得$\frac{{a}_{n}}{n}=2-\frac{1}{{2}^{n-1}}$,
∴${a}_{n}=2n-\frac{n}{{2}^{n-1}}$,
Sn=a1+a2+…+an
=$2×1-\frac{1}{{2}^{0}}+2×2-\frac{2}{{2}^{1}}+…+2n-\frac{n}{{2}^{n-1}}$=2(1+2+…+n)-($\frac{1}{{2}^{0}}+\frac{2}{{2}^{1}}+…+\frac{n}{{2}^{n-1}}$)
=n(n+1)-Tn,
${T}_{n}=\frac{1}{{2}^{0}}+\frac{2}{{2}^{1}}+…+\frac{n}{{2}^{n-1}}$,
则$\frac{1}{2}{T}_{n}=\frac{1}{{2}^{1}}+\frac{2}{{2}^{2}}+…+\frac{n}{{2}^{n}}$,
两式作差得:$\frac{1}{2}{T}_{n}=1+\frac{1}{2}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{n-1}}-\frac{n}{{2}^{n}}$=$\frac{1×(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}-\frac{n}{{2}^{n}}$=$2-\frac{n+2}{{2}^{n}}$,
∴${T}_{n}=4-\frac{n+2}{{2}^{n-1}}$,
∴${S}_{n}=n(n+1)-4+\frac{n+2}{{2}^{n-1}}$;
(3)证明:Sn-n(n+1)=$\frac{n+2}{{2}^{n-1}}-4$.
当n=1时,$\frac{1+2}{{2}^{0}}-4=-1≤-1$成立;
假设当n=k时不等式成立,即$\frac{k+2}{{2}^{k-1}}-4≤-1$,也就是$\frac{k+2}{{2}^{k-1}}≤3$,
难么,当n=k+1时,$\frac{k+1+2}{{2}^{k+1-1}}-4=\frac{k+3}{{2}^{k}}-4$=$\frac{k+3}{2(k+2)}•\frac{k+2}{{2}^{k-1}}-4$$≤3•\frac{k+3}{2(k+2)}-4=\frac{-5k-7}{2k+4}$.
要证$\frac{-5k-7}{2k+4}≤-1$,需证$\frac{5k+7}{2k+4}≥1$,即证5k+7≥2k+4,也就是证k≥1,此时显然成立.
∴当n=k+1时,不等式成立.
综上,不等式对于任意的n∈N*都成立.
点评 本题考查了累积法求数列的通项公式,训练了错位相减法求数列的和,训练了利用数学归纳法证明数列不等式,属中高档题.

 阅读快车系列答案
阅读快车系列答案| A. | (0,$\frac{π}{6}$] | B. | [$\frac{π}{3}$,$\frac{2π}{3}$] | C. | (0,$\frac{π}{3}$] | D. | [$\frac{2π}{3}$,π) |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
 如图,在长方体ABCD-A1B1C1D1中,点E,F分别是棱AB,BC的中点,点E1,F1分别是棱A1D1,C1D1的中点.求证:EE1∥FF1.
如图,在长方体ABCD-A1B1C1D1中,点E,F分别是棱AB,BC的中点,点E1,F1分别是棱A1D1,C1D1的中点.求证:EE1∥FF1.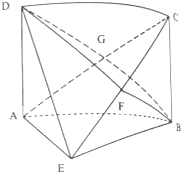 如图,在四棱锥E-ABCD中,地面ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC与BD相交于点G.
如图,在四棱锥E-ABCD中,地面ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC与BD相交于点G. 如图所示的一块木料中,棱BC平行于面A′C′.
如图所示的一块木料中,棱BC平行于面A′C′.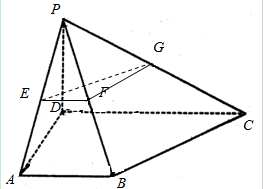 如图,在四棱锥P-ABCD的底面为直角梯形,且∠BAD=∠ADC=90°,E,F,G分别为PA,PB,PC的中点,直线PB⊥平面EFG,AB=$\frac{1}{3}$DC=$\frac{1}{3}$AD=1.
如图,在四棱锥P-ABCD的底面为直角梯形,且∠BAD=∠ADC=90°,E,F,G分别为PA,PB,PC的中点,直线PB⊥平面EFG,AB=$\frac{1}{3}$DC=$\frac{1}{3}$AD=1.