Question

（本小题满分14分）如图, 在直三棱柱ABC－A₁B₁C₁中，AC＝3，BC＝4，，AA₁＝4，点D是AB的中点。

（1）求证：AC ⊥ BC₁；

（2）求证：AC ₁  // 平面CDB₁；

（3）求多面体的体积。

 

Answer 1

【答案】

解：（1）∵底面三边长AC=3，BC=4，AB=5，∴ AC⊥BC，       （2分）

又在直三棱柱ABC－A₁B₁C₁中，CC₁⊥底面ABC，AC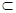底面ABC，∴CC₁⊥AC，（3分）

BC、CC₁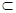平面BCC₁，且BC 与CC₁相交       ∴ AC⊥平面BCC₁；（5分）

而BC₁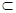平面BCC₁                           ∴ AC⊥BC₁                        （6分）

（2）设CB₁与C₁B的交点为E，连结DE，

∵ D是AB的中点，E是BC₁的中点，   ∴ DE//AC₁，   （8分）

∵ DE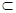平面CDB₁，AC₁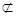平面CDB₁，     ∴ AC₁//平面CDB₁    （10分）

（3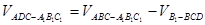）  （11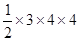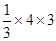分）=-   （13分）

=20                                                    （14分）

【解析】略