题目内容
【题目】由不等式组  确定的平面区域记为Ω1 , 不等式组
确定的平面区域记为Ω1 , 不等式组 ![]() 确定的平面区域记为Ω2 , 在Ω1中随机取一点,则该点恰好在Ω2内的概率为( )
确定的平面区域记为Ω2 , 在Ω1中随机取一点,则该点恰好在Ω2内的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:平面区域Ω1 , 为三角形AOB,面积为 ![]() ,
,
平面区域Ω2 , 为△AOB内的四边形BDCO,
其中C(0,1),
由 ![]() ,解得
,解得  ,即D(
,即D( ![]() ,
, ![]() ),
),
则三角形ACD的面积S= ![]() =
= ![]() ,
,
则四边形BDCO的面积S= ![]() ,
,
则在Ω1中随机取一点,则该点恰好在Ω2内的概率为 ![]() ,
,
故选:D.
【考点精析】本题主要考查了几何概型的相关知识点,需要掌握几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等才能正确解答此题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
【题目】某班![]() 名同学的数学小测成绩的频率分布表如图所示,其中
名同学的数学小测成绩的频率分布表如图所示,其中![]() ,且分数在
,且分数在![]() 的有
的有![]() 人.
人.
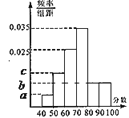
(1)求![]() 的值;
的值;
(2)若分数在![]() 的人数是分数在
的人数是分数在![]() 的人数的
的人数的![]() ,求从不及格的人中任意选取3人,其中分数在50分以下的人数为
,求从不及格的人中任意选取3人,其中分数在50分以下的人数为![]() ,求
,求![]() 的数学期.
的数学期.
【题目】通过随机询问72名不同性别的大学生在购买食物时是否看营养说明,得到如下列联表:
男 | 女 | 总计 | ||
读营养说明 | 16 | 28 | 44 | |
不读营养说明 | 20 | 8 | 28 | |
总计 | 36 | 36 | 72 |
(1)根据以上列联表判断,能否在犯错误的概率不超过0.005的前提下认为性别和是否看营养说明有关系呢?
(2)从被询问的28名不读营养说明的大学生中,随机抽取2名学生,求抽到女生人数![]()
的分布列及数学期望.
附:
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
![]()