题目内容
向量a=(cos23°,cos67°),向量b=(cos68°,cos22°).
(1)求a·b;
(2)若向量b与向量m共线,u=a+m,求u的模的最小值.
(1)求a·b;
(2)若向量b与向量m共线,u=a+m,求u的模的最小值.
(1)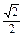 (2)
(2)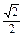
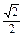 (2)
(2)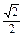
(1)a·b=cos23°·cos68°+cos67°·cos22°
=cos23°·sin22°+sin23°·cos22°=sin45°=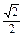 .
.
(2)由向量b与向量m共线,
得m= b(
b( ∈R),
∈R),
u=a+m=a+ b
b
=(cos23°+ cos68°,cos67°+
cos68°,cos67°+ cos22°)
cos22°)
=(cos23°+ sin22°,sin23°+
sin22°,sin23°+ cos22°),
cos22°),
|u|2=(cos23°+ sin22°)2+(sin23°+
sin22°)2+(sin23°+ cos22°)2
cos22°)2
= 2+
2+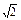
 +1=
+1=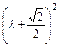 +
+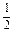 ,
,
∴当 =-
=-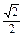 时,|u|有最小值为
时,|u|有最小值为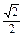 .
.
=cos23°·sin22°+sin23°·cos22°=sin45°=
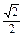 .
.(2)由向量b与向量m共线,
得m=
 b(
b( ∈R),
∈R),u=a+m=a+
 b
b=(cos23°+
 cos68°,cos67°+
cos68°,cos67°+ cos22°)
cos22°)=(cos23°+
 sin22°,sin23°+
sin22°,sin23°+ cos22°),
cos22°),|u|2=(cos23°+
 sin22°)2+(sin23°+
sin22°)2+(sin23°+ cos22°)2
cos22°)2=
 2+
2+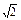
 +1=
+1=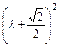 +
+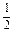 ,
,∴当
 =-
=-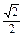 时,|u|有最小值为
时,|u|有最小值为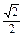 .
.
练习册系列答案
相关题目
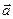 =(-1,x)与
=(-1,x)与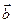 ="(-x," 2)共线且方向相同,求x
="(-x," 2)共线且方向相同,求x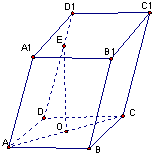
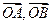 满足
满足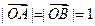 ,
,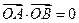 ,
,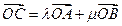
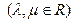 若
若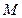 为
为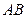 的中点,并且
的中点,并且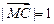 ,则点
,则点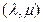 在( )
在( )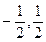 )为圆心,半径为1的圆上
)为圆心,半径为1的圆上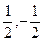 )为圆心,半径为1的圆上
)为圆心,半径为1的圆上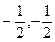 )为圆心,半径为1的圆上
)为圆心,半径为1的圆上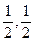 )为圆心,半径为1的圆上
)为圆心,半径为1的圆上 ,
, ,若
,若 平行,则λ= .
平行,则λ= .
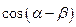 =
= 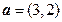 ,
,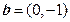 ,那么向量
,那么向量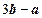 的坐标是_____________.
的坐标是_____________.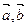 中,已知
中,已知 ,
,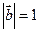 ,且
,且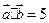 ,则向量
,则向量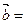 ______。
______。