题目内容
【题目】设![]() 是定义在
是定义在![]() 上的偶函数,
上的偶函数, ![]() ,都有
,都有![]() ,且当
,且当![]() 时,
时, ![]() ,若函数
,若函数![]() (
(![]() )在区间
)在区间![]() 内恰有三个不同零点,则实数
内恰有三个不同零点,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】A
【解析】由![]() 可得函数
可得函数![]() 的图象关于
的图象关于![]() 对称,即
对称,即![]()
又函数![]() 是偶函数,则
是偶函数,则![]() ,
,
∴![]() ,即函数的周期是4.
,即函数的周期是4.
当![]() 时,
时, ![]() ,此时
,此时![]() ,
,
由![]() 得
得![]() ,令
,令![]() .
.
∵函数![]() (
(![]() )在区间
)在区间![]() 内恰有三个不同零点,
内恰有三个不同零点,
∴函数![]() 和
和![]() 的图象在区间
的图象在区间![]() 内有三个不同的公共点.
内有三个不同的公共点.
作出函数![]() 的图象如图所示.
的图象如图所示.

①当![]() 时,函数
时,函数![]() 为增函数,
为增函数,
结合图象可得,要使两函数的图象有三个公共点,则需满足![]() 在点A处的函数值小于2,在点B处的函数值大于2,
在点A处的函数值小于2,在点B处的函数值大于2,
即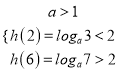 ,解得
,解得![]() ;
;
②当![]() 时,函数
时,函数![]() 为减函数,
为减函数,
结合图象可得,要使两函数的图象有三个公共点,则需满足![]() 在点C处的函数值小于
在点C处的函数值小于![]() ,在点B处的函数值大于
,在点B处的函数值大于![]() ,
,
即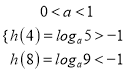 ,解得
,解得![]() .
.
综上可得实数![]() 的取值范围是
的取值范围是![]() .选A.
.选A.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目