题目内容
一动圆截直线 和直线
和直线 所得弦长分别为
所得弦长分别为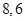 ,求动圆圆心的轨迹方程。
,求动圆圆心的轨迹方程。
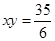
解析试题分析:设动圆圆心为M,由动圆截两直线所得的弦长,结合点到直线的距离公式,根据半径相等列关于动圆圆心坐标的关系式,整理后得答案.
试题解析:设动圆圆心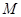 点的坐标为
点的坐标为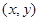 ,
,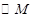 分别截直线
分别截直线 和
和 所得弦分别为
所得弦分别为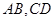 ,则
,则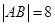 ,
,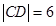 ,过
,过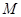 分别作直线
分别作直线 和
和 的垂线,垂足分别为
的垂线,垂足分别为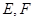 ,则
,则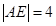 ,
,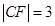 ,
,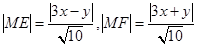 ,
,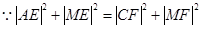 ,
, 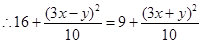 ,
, 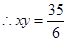 ,所以动圆圆心的轨迹方程是
,所以动圆圆心的轨迹方程是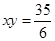 .
.
考点:轨迹方程.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 +y2=1.过
+y2=1.过 轴上的动点
轴上的动点 (m,0)作圆x2+y2=1的切线l交椭圆G于A,B两点.
(m,0)作圆x2+y2=1的切线l交椭圆G于A,B两点. 的最大距离;
的最大距离;  时,求A,B两点坐标;
时,求A,B两点坐标; :
: ,点
,点 ,直线
,直线 .
.
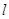 垂直的直线方程;
垂直的直线方程; 上(
上( 为坐标原点),存在定点
为坐标原点),存在定点 (不同于点
(不同于点 ),满足:对于圆
),满足:对于圆 ,都有
,都有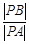 为一常数,试求出所有满足条件的点
为一常数,试求出所有满足条件的点 .求动点M的轨迹方程,并说明它表示什么.
.求动点M的轨迹方程,并说明它表示什么.
 内有一点
内有一点 ,
, 为过点
为过点 且倾斜角为
且倾斜角为 的弦.
的弦.
 时,求
时,求 ;
; ,求点
,求点 的圆心与点
的圆心与点 关于直线
关于直线 对称,直线
对称,直线 与圆
与圆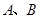 两点,且
两点,且 ,求圆
,求圆
 )满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为
)满足到定点A(-1,0)的距离与到定点B(1,0)距离之比为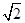
 与曲线C交于两点M、N,若|MN|=4,求直线
与曲线C交于两点M、N,若|MN|=4,求直线 的方程。
的方程。 上的圆C.
上的圆C. 轴相切时,求圆C的方程;
轴相切时,求圆C的方程; ,求圆心的横坐标
,求圆心的横坐标 的取值范围.
的取值范围.