题目内容
数列{an}的前n项和Sn满足Sn+1=a2Sn+a1,其中a2≠0。
(I)求证:{an}是首项为1的等比数列;
(II)若a2>-1,求证: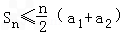 并给出等号成立的充要条件。
并给出等号成立的充要条件。
(I)求证:{an}是首项为1的等比数列;
(II)若a2>-1,求证:
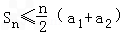 并给出等号成立的充要条件。
并给出等号成立的充要条件。证明:(I)∵Sn+1=a2Sn+a1,①
∴Sn+2=a2Sn+1+a1,②
①﹣②可得:an+2=a2an+1
∵a2≠0,
∴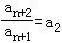
∵Sn+1=a2Sn+a1,
∴S2=a2S1+a1,
∴a2=a2a1
∵a2≠0,
∴a1=1
∴{an}是首项为1的等比数列。
(II)当n=1或2时,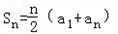 等号成立
等号成立
设n≥3,a2>-1,且a2≠0,
由(I)知a1=1,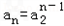 ,
,
所以要证的不等式可化为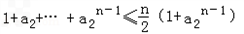 (n≥3)
(n≥3)
即证 (n≥2)
(n≥2)
a2=1时,等号成立当
-1<a2<1时,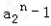 与
与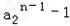 同为负;
同为负;
当a2>1时,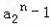 与
与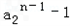 同为正;
同为正;
∴a2>-1且a2≠1时,(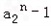 )(
)(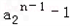 )>0,
)>0,
即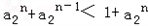 上面不等式n分别取1,2,…,n累加可得
上面不等式n分别取1,2,…,n累加可得 ?
?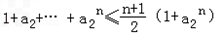
综上,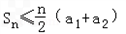 ,等号成立的充要条件是n=1或2或a2=1。
,等号成立的充要条件是n=1或2或a2=1。
∴Sn+2=a2Sn+1+a1,②
①﹣②可得:an+2=a2an+1
∵a2≠0,
∴
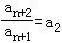
∵Sn+1=a2Sn+a1,
∴S2=a2S1+a1,
∴a2=a2a1
∵a2≠0,
∴a1=1
∴{an}是首项为1的等比数列。
(II)当n=1或2时,
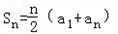 等号成立
等号成立设n≥3,a2>-1,且a2≠0,
由(I)知a1=1,
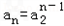 ,
,所以要证的不等式可化为
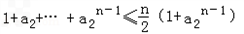 (n≥3)
(n≥3)即证
 (n≥2)
(n≥2)a2=1时,等号成立当
-1<a2<1时,
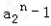 与
与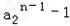 同为负;
同为负;当a2>1时,
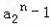 与
与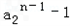 同为正;
同为正;∴a2>-1且a2≠1时,(
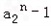 )(
)(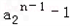 )>0,
)>0,即
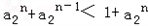 上面不等式n分别取1,2,…,n累加可得
上面不等式n分别取1,2,…,n累加可得 ?
?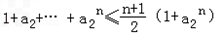
综上,
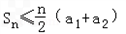 ,等号成立的充要条件是n=1或2或a2=1。
,等号成立的充要条件是n=1或2或a2=1。
练习册系列答案
相关题目