题目内容
已知函数
(1)求函数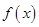 的最大值;
的最大值;
(2)若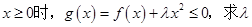 的取值范围.
的取值范围.
(1)0;(2)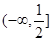
解析试题分析:(1)先求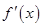 ,再利用
,再利用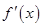 判断函数
判断函数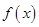 的单调性并求最值;
的单调性并求最值;
(2)由题设知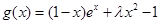 先求其导数得
先求其导数得
因为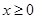 ,所以
,所以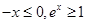 ,可分
,可分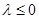 ,
,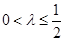 ,
,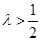 三种情况探究
三种情况探究 ,进而得到函数
,进而得到函数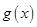 变化性质,并从中找出满足
变化性质,并从中找出满足 的
的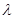 的取值范围.
的取值范围.
解:(1)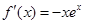 , 1分
, 1分
当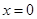 时,
时,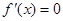 ;当
;当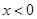 时,
时,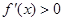 ;当
;当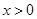 时,
时,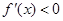 ;
;
所以函数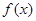 在区间
在区间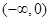 上单调递增,在区间
上单调递增,在区间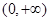 上单调递减; 3分
上单调递减; 3分
故 . 4分
. 4分
(2)由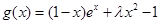 ,得
,得 . 6分
. 6分
当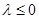 时,由(1)得
时,由(1)得 成立; 8分
成立; 8分
当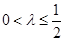 时,因为
时,因为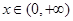 时
时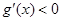 ,所以
,所以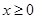 时,
时,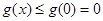 成立; 10分
成立; 10分
当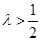 时,因为
时,因为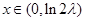 时
时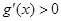 ,所以
,所以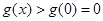 .13分
.13分
综上,知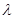 的取值范围是
的取值范围是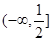 . 14分
. 14分
考点:1、导数在研究函数性质中的应用;2、分类讨论的思想.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
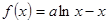 .
.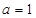 时,求
时,求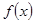 的极值;
的极值;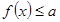 对
对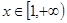 恒成立,求实数
恒成立,求实数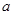 的取值范围.
的取值范围.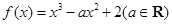 ,
,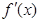 为
为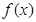 的导函数。 (1)求函数
的导函数。 (1)求函数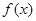 的单调递减区间;
的单调递减区间;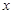 ,有
,有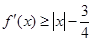 成立,求
成立,求 的取值范围;
的取值范围; 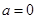 时,在曲线
时,在曲线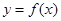 上是否存在两点
上是否存在两点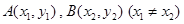 ,使得曲线在
,使得曲线在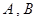 两点处的切线均与直线
两点处的切线均与直线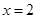 交于同一点?若存在,求出交点纵坐标的最大值;若不存在,请说明理由.
交于同一点?若存在,求出交点纵坐标的最大值;若不存在,请说明理由.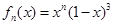 在
在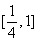 上的最大值为
上的最大值为 (
(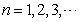 ).
).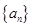 的通项公式;
的通项公式;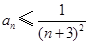 成立;
成立;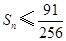 成立.
成立. ≈1.6,e0.3≈1.3)。
≈1.6,e0.3≈1.3)。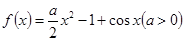 .
.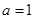 时,求函数
时,求函数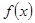 在
在 上的最大值和最小值;
上的最大值和最小值; 上为增函数,求正数
上为增函数,求正数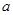 的取值范围.
的取值范围.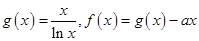 .
.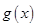 的单调区间;
的单调区间;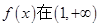 上是减函数,求实数a的最小值;
上是减函数,求实数a的最小值;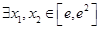 ,使
,使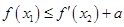 成立,求实数a的取值范围.
成立,求实数a的取值范围. 的取值范围.
的取值范围.