题目内容
15. 已知函数f(x)是定义域为R的偶函数,当x≥0时,f(x)=-x2+2x.
已知函数f(x)是定义域为R的偶函数,当x≥0时,f(x)=-x2+2x.(1)写出该函数的解析式;
(2)在给定的图示中画出函数f(x)的图象(不需列表);
(3)写出该函数值域,单调区间(不要求证明).
分析 (1)设x<0,则-x>0,根据函数f(x)为R上的偶函数,当x≥0时,f(x)=-x2+2x+1,可得函数解析式;
(2)根据函数的解析式,可得函数的图象;
(3)利用函数的图象,可得函数的单调区间与函数的值域.
解答 解:(1)设x<0,则-x>0
因为函数f(x)为R上的偶函数,所以f(x)=f(-x)=-x2-2x
所以f(x)=$\left\{\begin{array}{l}{-{x}^{2}+2x,x≥0}\\{-{x}^{2}-2x,x<0}\end{array}\right.$;
(2)函数f(x)的图象如图所示: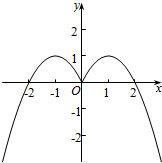
(3)由图象可知:f(x)的单调增区间为(-∞,-1),(0,1),f(x)的单调减区间为(-1,0),(1,+∞),f(x)的值域是(-∞,1].
点评 本题考查函数的解析式,考查函数的奇偶性,考查函数的图象,考查数形结合的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知a<b,则下列各式正确的是( )
| A. | a2<b2 | B. | ac<bc | C. | log2a<log2b | D. | 2a<2b |
10.下列椭圆中最接近于圆的是( )
| A. | 4x2+9y2=36 | B. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{20}$=1 | C. | 9x2+4y2=36 | D. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{16}$=1 |