题目内容
【题目】选修4-4:坐标系与参数方程
已知圆![]() 在极坐标方程为
在极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).若直
为参数).若直
线![]() 与圆
与圆![]() 相交于不同的两点
相交于不同的两点![]() .
.
(Ⅰ)写出圆![]() 的直角坐标方程,并求圆心的坐标与半径;
的直角坐标方程,并求圆心的坐标与半径;
(Ⅱ)若弦长![]() ,求直线
,求直线![]() 的斜率.
的斜率.
【答案】(I)![]() ;(II)
;(II)![]() 或
或![]() .
.
【解析】
试题分析:(I)化极坐标方程为直角坐标方程主要是利用公式![]() ,
,![]() ,
,![]() 来完成.代入可得
来完成.代入可得![]() ,配方得
,配方得![]() ,所以圆心为
,所以圆心为![]() ,半径为
,半径为![]() ;(II)在极坐标方程与参数方程的条件下求解直线与圆的位置关系问题,通常将极坐标方程与参数方程均化为直角坐标方程来解决. 由直线
;(II)在极坐标方程与参数方程的条件下求解直线与圆的位置关系问题,通常将极坐标方程与参数方程均化为直角坐标方程来解决. 由直线![]() 的参数方程知直线过定点
的参数方程知直线过定点![]() ,直线
,直线![]() 的方程为
的方程为![]() .利用弦长等于
.利用弦长等于![]() 可求得斜率
可求得斜率![]() 或
或![]() .
.
试题解析:(I)由![]() ,得
,得![]() .
.
将![]() ,代入可得
,代入可得![]() ,
,
配方,得![]() ,所以圆心为
,所以圆心为![]() ,半径为
,半径为![]() .
.
(II)由直线![]() 的参数方程知直线过定点
的参数方程知直线过定点![]() ,
,
则由题意,知直线![]() 的斜率一定存在,因此不妨设直线
的斜率一定存在,因此不妨设直线![]() 的方程为
的方程为![]() 的方程为
的方程为![]() .
.
因为![]() ,所以
,所以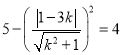 ,解得
,解得![]() 或
或![]() .
.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
【题目】某数学教师对所任教的两个班级各抽取20名学生进行测试,分数分布如表:
分数区间 | 甲班频率 | 乙班频率 |
| 0.1 | 0.2 |
| 0.2 | 0.2 |
| 0.3 | 0.3 |
| 0.2 | 0.2 |
| 0.2 | 0.1 |
(Ⅰ)若成绩120分以上(含120分)为优秀,求从乙班参加测试的90分以上(含90分)的同学中,随机任取2名同学,恰有1人为优秀的概率;
(Ⅱ)根据以上数据完成下面的![]() ×
×![]() 列联表:
列联表:
优秀 | 不优秀 | 总计 | |
甲班 | |||
乙班 | |||
总计 |
在犯错概率小于0.1的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系?
参考公式: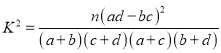 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|