题目内容
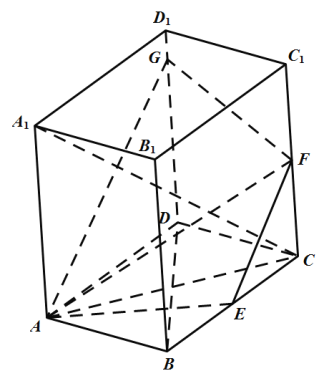
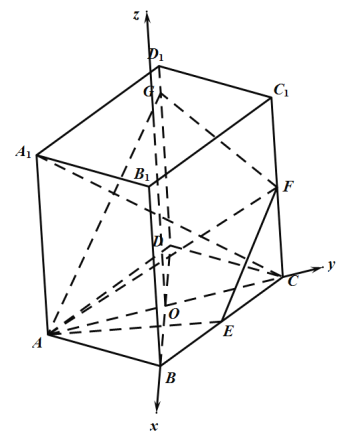
【题目】如图,直四棱柱![]() 的底面
的底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() .
.![]() 、
、![]() 分别为
分别为![]() 和
和![]() 的中点.平面
的中点.平面![]() 与棱
与棱![]() 所在直线交于点
所在直线交于点![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)判断点![]() 是否与点
是否与点![]() 重合.
重合.
【答案】(1)证明见解析(2)![]() (3)
(3)![]() 与
与![]() 重合.
重合.
【解析】
(1)在平面![]() 中,利用菱形的性质可以证明出
中,利用菱形的性质可以证明出![]() ,结合直棱柱的性质、线面垂直的性质定理可以证明出
,结合直棱柱的性质、线面垂直的性质定理可以证明出![]() ,这样利用线面垂直、面面垂直的判定定理证明出平面
,这样利用线面垂直、面面垂直的判定定理证明出平面![]() 平面
平面![]() ;
;
(2)建立空间直角坐标系,利用空间向量夹角公式求出直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)通过空间向量数量积公式可得![]() ,利用线面的相交关系,可以证明出点
,利用线面的相交关系,可以证明出点![]() 与点
与点![]() 重合.或者通过设点
重合.或者通过设点![]() 的坐标,通过空间向量数量积公式,由
的坐标,通过空间向量数量积公式,由![]() ,可以求出
,可以求出![]() 的坐标,这样就可以证明出点
的坐标,这样就可以证明出点![]() 与点
与点![]() 重合.
重合.
证明:(1)如图所示,连结![]() ,
,![]() ,
,
∵四边形![]() 为菱形,
为菱形,
且![]() ,∴
,∴![]() ,
,
又![]() 为等边
为等边![]() 的边
的边![]() 的中点,
的中点,
∴![]() .
.
又直四棱柱中,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
∴![]() .
.
又![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(2)法1:
∵![]() ,
,![]() ,
,![]() 三线垂直,
三线垂直,
∴以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 所在的直线为
所在的直线为![]() ,
,![]() ,
,![]() 轴建系,则
轴建系,则
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则
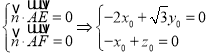 ,
,
令![]() 得
得![]() .
.
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则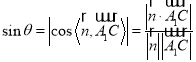
 .
.
∴直线![]() 与平面所成角正弦值为
与平面所成角正弦值为![]() .
.
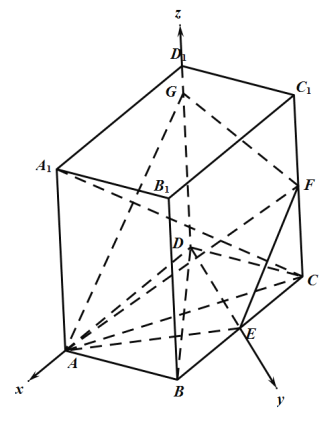
法2:
如图所示,连结![]() ,
,![]() 交于点
交于点![]() .连接
.连接![]() ,
,![]() 交于
交于![]() ,
,
∵四边形![]() 为菱形,∴
为菱形,∴![]() ,
,
又![]() ,
,![]() 底面
底面![]() ,∴
,∴![]() 平面
平面![]() .
.
易得![]() ,
,![]() ,
,![]() 三线垂直,如图所示.
三线垂直,如图所示.
以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() ,
,![]() ,
,![]() 轴建系,
轴建系,
则![]() ,
,![]() ,
,![]() ,
, ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则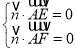 ,即
,即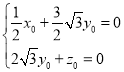 ,
,
令![]() 得
得![]() ,
,
∴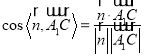
![]() ,
,
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
则![]() .
.
(3)法1:![]() ,
,![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
又![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
即![]() 平面
平面![]() ,
,
由已知![]() 平面
平面![]() ,
,
且![]() 平面
平面![]() ,
,
∴![]() 与
与![]() 点重合.
点重合.
法2:设![]() .
.
则![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,又
,又![]() ,
,
即![]() 与
与![]() 重合.
重合.

 备战中考寒假系列答案
备战中考寒假系列答案【题目】2019年5月,重庆市育才中学开展了“最美教室”文化布置评比活动,工作人员随机抽取了16间教室进行量化评估,其中评分不低于9分的教室评为优秀,以下表格记录了它们的评分情况:
分数段 |
|
|
|
|
教室间数 | 1 | 3 | 8 | 4 |
(1)现从16间教室随机抽取3个,求至多有1个优秀的概率;
(2)以这16间教室评分数据估计全校教室的布置情况,若从全校所有教室中任选3个,记![]() 表示抽到优秀的教室个数,求
表示抽到优秀的教室个数,求![]() 的分布列及数学期望.
的分布列及数学期望.
【题目】中国大学先修课程,是在高中开设的具有大学水平的课程,旨在让学有余力的高中生早接受大学思维方式、学习方法的训练,为大学学习乃至未来的职业生涯做好准备.某高中开设大学先修课程已有两年,两年共招收学生2000人,其中有300人参与学习先修课程,两年全校共有优等生200人,学习先修课程的优等生有60人.这两年学习先修课程的学生都参加了考试,并且都参加了某高校的自主招生考试(满分100分),结果如下表所示:
分数 |
|
|
|
|
|
人数 | 20 | 55 | 105 | 70 | 50 |
参加自主招生获得通过的概率 | 0.9 | 0.8 | 0.6 | 0.5 | 0.4 |
(1)填写列联表,并画出列联表的等高条形图,并通过图形判断学习先修课程与优等生是否有关系,根据列联表的独立性检验,能否在犯错误的概率不超过0.01的前提下认为学习先修课程与优等生有关系?
优等生 | 非优等生 | 总计 | |
学习大学先修课程 | |||
没有学习大学先修课程 | |||
总计 |
(2)已知今年有150名学生报名学习大学先修课程,以前两年参加大学先修课程学习成绩的频率作为今年参加大学先修课程学习成绩的概率.
①在今年参与大学先修课程的学生中任取一人,求他获得某高校自主招生通过的概率;
②设今年全校参加大学先修课程的学生获得某高校自主招生通过的人数为![]() ,求
,求![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式:![]() ,其中
,其中![]() .
.
【题目】2019年1月1日起新的个人所得税法开始实施,依据《中华人民共和国个人所得税法》可知纳税人实际取得工资、薪金(扣除专项、专项附加及依法确定的其他)所得不超过5000元(俗称“起征点”)的部分不征税,超出5000元部分为全月纳税所得额.新的税率表如下:
2019年1月1日后个人所得税税率表
全月应纳税所得额 | 税率(%) |
不超过3000元的部分 | 3 |
超过3000元至12000元的部分 | 10 |
超过12000元至25000元的部分 | 20 |
超过25000元至35000元的部分 | 25 |
个人所得税专项附加扣除是指个人所得税法规定的子女教育、继续教育、大病医疗、住房贷款利息、住房租金和赡养老人等六项专项附加扣除.其中赡养老人一项指纳税人赡养60岁(含)以上父母及其他法定赡养人的赡养支出,可按照以下标准扣除:纳税人为独生子女的,按照每月2000元的标准定额扣除;纳税人为非独生子女的,由其与兄弟姐妹分摊每月2000元的扣除额度,每人分摊的额度不能超过每月1000元.某纳税人为独生子,且仅符合规定中的赡养老人的条件,如果他在2019年10月份应缴纳个人所得税款为390元,那么他当月的工资、薪金税后所得是______元.