题目内容
设直线l与曲线f(x)=x3+2x+1有三个不同的交点A、B、C,且︱AB︱=︱BC︱=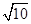 ,则直线l的方程为( )
,则直线l的方程为( )
A.y=5x+1 B.y=4x+1 C.y=3x+1 D.y=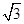 x+1
x+1
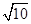 ,则直线l的方程为( )
,则直线l的方程为( )A.y=5x+1 B.y=4x+1 C.y=3x+1 D.y=
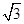 x+1
x+1C
由曲线 关于(0,1)中心对称,则B(0,1),设直线l的方程为y=kx+1,
关于(0,1)中心对称,则B(0,1),设直线l的方程为y=kx+1,
代入y=x3+2x+1,可得x3=(k-2)x,∴x=0或x=± ,∴不妨设A(
,∴不妨设A( ,k·
,k· +1)(k
+1)(k
>2),∵|AB|=|BC|=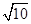 ∴(
∴( -0)2+ (k·
-0)2+ (k· +1-1)2=10错误!链接无效。∴k3-2k2+k-12=0,
+1-1)2=10错误!链接无效。∴k3-2k2+k-12=0,
∴(k-3)(k2+k+4)=0,解得k=3,∴直线l的方程为y=3x+1,故选C.
 关于(0,1)中心对称,则B(0,1),设直线l的方程为y=kx+1,
关于(0,1)中心对称,则B(0,1),设直线l的方程为y=kx+1,代入y=x3+2x+1,可得x3=(k-2)x,∴x=0或x=±
 ,∴不妨设A(
,∴不妨设A( ,k·
,k· +1)(k
+1)(k>2),∵|AB|=|BC|=
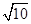 ∴(
∴( -0)2+ (k·
-0)2+ (k· +1-1)2=10错误!链接无效。∴k3-2k2+k-12=0,
+1-1)2=10错误!链接无效。∴k3-2k2+k-12=0,∴(k-3)(k2+k+4)=0,解得k=3,∴直线l的方程为y=3x+1,故选C.

练习册系列答案
相关题目
 ,则下列说法错误的是( )
,则下列说法错误的是( ) ,则
,则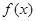 有零点
有零点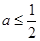 且
且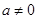
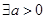 使得
使得 在
在 内有解,则
内有解,则 的图象可能是( )
的图象可能是( )
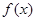 与
与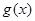 的图像在
的图像在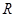 上不间断,由下表知方程f(x)=g(x)有实数解的区间是( )
上不间断,由下表知方程f(x)=g(x)有实数解的区间是( ) 是定义在
是定义在 上的奇函数,其图象如图所示,令
上的奇函数,其图象如图所示,令 ,则下列关于函数
,则下列关于函数 的叙述正确的是()
的叙述正确的是()
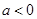 ,则函数
,则函数 ,则方程
,则方程 有大于2的实根
有大于2的实根 ,则方程
,则方程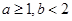 ,则方程
,则方程 方程
方程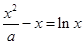 有唯一的解,则实数
有唯一的解,则实数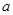 的取值范围是________.
的取值范围是________. 和
和 ,定义运算“
,定义运算“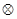 ”:
”: =
= .设函数
.设函数
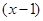 ,
, .若函数
.若函数 的图象与
的图象与 轴恰有两个公共点,则实数
轴恰有两个公共点,则实数 的取值范围是___________.
的取值范围是___________.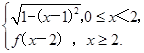 若关于x的方程f(x)=kx(k>0)有且仅有四个根,其最大根为t,则函数g(t)=
若关于x的方程f(x)=kx(k>0)有且仅有四个根,其最大根为t,则函数g(t)=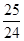 t2-6t+7的值域为________.
t2-6t+7的值域为________.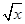 ,那么在区间(-1,3)内,关于x的方程f(x)=kx+k(k∈R)有4个根,则k的取值范围是( ).
,那么在区间(-1,3)内,关于x的方程f(x)=kx+k(k∈R)有4个根,则k的取值范围是( ).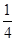 或k=
或k=