题目内容
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为:
的参数方程为: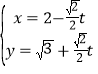 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与直线
与直线![]() 交于
交于![]() 两点,若点
两点,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() .
.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】试题分析:
(1)消去参数可得直线![]() 的普通方程为
的普通方程为![]() ,极坐标化为直角坐标可得曲线
,极坐标化为直角坐标可得曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)将直线![]() 的参数方程代入曲线
的参数方程代入曲线![]() 的直角坐标方程,可得
的直角坐标方程,可得![]() ,结合参数方程的几何意义可知
,结合参数方程的几何意义可知![]() .
.
试题解析:
(1)由直线![]() 的参数方程:
的参数方程: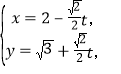 得直线
得直线![]() 的普通方程为
的普通方程为![]() ,
,
由![]() 得
得![]() ,配方得
,配方得![]() ,
,
即曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)将直线![]() 的参数方程代入曲线
的参数方程代入曲线![]() 的直角坐标方程,得
的直角坐标方程,得![]() ,
,
即![]() ,
,
因为![]() ,所以可设
,所以可设![]() 是点
是点![]() 所对应的参数,则
所对应的参数,则![]() .
.
又直线过点![]() ,所以
,所以![]() .
.

练习册系列答案
相关题目
【题目】为了调查某社区居民每天参加健身的时间,某机构在该社区随机采访男性、女性各50名,其中每人每天的健身时间不少于1小时称为“健身族”,否则称其为"非健身族”,调查结果如下:
健身族 | 非健身族 | 合计 | |
男性 | 40 | 10 | 50 |
女性 | 30 | 20 | 50 |
合计 | 70 | 30 | 100 |
(1)若居民每人每天的平均健身时间不低于70分钟,则称该社区为“健身社区”. 已知被随机采访的男性健身族,男性非健身族,女性健身族,女性非健身族每人每天的平均健分时间分別是1.2小时,0.8小时,1.5小时,0.7小时,试估计该社区可否称为“健身社区”?
(2)根据以上数据,能否在犯错误的概率不超过5%的情况下认为“健身族”与“性别”有关?
参考公式: 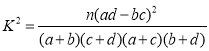 ,其中
,其中![]() .
.
参考数据:
| 0. 50 | 0. 40 | 0. 25 | 0. 05 | 0. 025 | 0. 010 |
| 0. 455 | 0. 708 | 1. 321 | 3. 840 | 5. 024 | 6. 635 |