题目内容
6.下列几个命题,其中正确的有(1)(2)(3)(4)(5)(请把正确命题的所有序号都写上!)(1)函数$y=\frac{{\sqrt{x+1}}}{x}$的定义域为{x|x≥-1但x≠0};
(2)已知f(x)=ax2+bx是定义在[b-1,2b]上的奇函数,那么$a+b=\frac{1}{3}$;
(3)已知f(x)=ax5+bx3+cx-8,且f(2013)=2016,则f(-2013)=-2032;
(4)函数y=|x2-3x+2|的图象和直线y=m有两个公共点,则m的范围是$\left\{0\right\}∪(\frac{1}{4},+∞)$;
(5)定义在R上的函数f(x)的值域是[-1,2],则函数f(x+2013)的值域仍为[-1,2].
分析 求出函数的定义域,可判断(1);根据奇函数的定义,求出a,b值,可判断(2):构造奇函数g(x)=f(x)+8,进而求出f(-2013),可判断(3);画出函数y=|x2-3x+2|的图象,数形结合,可判断(4);根据左右平移变换不改变函数的值域,可判断(5).
解答 解:由$\left\{\begin{array}{l}x+1≥0\\ x≠0\end{array}\right.$得:x≥-1但x≠0,故(1)函数$y=\frac{{\sqrt{x+1}}}{x}$的定义域为{x|x≥-1但x≠0}正确;
若f(x)=ax2+bx是定义在[b-1,2b]上的奇函数,则a=0,b-1+2b=0,即a=0,b=$\frac{1}{3}$,故(2)$a+b=\frac{1}{3}$正确;
令g(x)=f(x)+8=ax5+bx3+cx,则g(x)为奇函数,由f(2013)=2016可得g(2013)=2024,进而g(-2013)=-2024,故(3)f(-2013)=-2032正确;
函数y=|x2-3x+2|的图象如下图所示: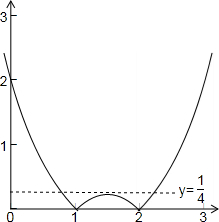
由图可得:m∈$\left\{0\right\}∪(\frac{1}{4},+∞)$时,函数y=|x2-3x+2|的图象和直线y=m有两个公共点,故(4)正确;
函数f(x+2013)的图象由函数f(x)的图象向左平移2013个单位得到,值域不变,故(5)正确;
故正确的命题为:(1)(2)(3)(4)(5),
故答案为:(1)(2)(3)(4)(5)
点评 本题以命题的真假判断为载体,考查了函数的定义域,值域,平移变换,奇偶性,零点,等知识点,难度中档.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
17.数列{an}中,已知a1=1,an+1=-$\frac{1}{{a}_{n}+1}$,则a2015=( )
| A. | -2 | B. | -$\frac{1}{3}$ | C. | 1 | D. | -$\frac{1}{2}$ |