题目内容
15．设正项等差数列{an}的前n项和为Sn，若S2015=2015，则$\frac{1}{a_2}+\frac{1}{{{a_{2014}}}}$的最小值为（ ）| A． | 1 | B． | 2 | C． | 4 | D． | 8 |
分析 由已知条件利用等差数列的性质得a2+a2014=2，由此利用均值定理能求出$\frac{1}{a_2}+\frac{1}{{{a_{2014}}}}$的最小值．
解答 解：∵等差数列{an}的前n项和为Sn，an＞0，且S2015=2015，
∴a1+a2015=a2+a2014=2，
∴a2•a2014≤$（\frac{{a}_{2}+{a}_{2014}}{2}）^{2}$=1，
∴$\frac{1}{a_2}+\frac{1}{{{a_{2014}}}}$=$\frac{{a}_{2014}+{a}_{2}}{{a}_{2}•{a}_{2014}}$=$\frac{2}{{a}_{2}•{a}_{2014}}$≥2，
当且仅当a2=a2014=1时取等号，
∴$\frac{1}{a_2}+\frac{1}{{{a_{2014}}}}$的最小值为2．
故选：B．
点评 本题考查等差数列中两项倒数和的最小值的求法，是基础题，解题时要注意等差数列的性质和均值定理的合理运用．
练习册系列答案
相关题目
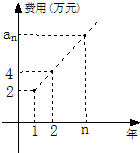某公司今年年初用25万元引进一种新的设备，投入设备后每年收益为21万元．该公司第n年需要支付设备的维修和工人工资等费用an的信息如图．
7．命题“?x0∈R，使得x2=1”的否定是（ ）
| A． | ?x∈R，都有x2=1 | B． | ?x0∉R，使得x2=1 | C． | ?x∈R，都有x2≠1 | D． | ?x0∈R，使得x2≠1 |