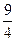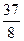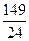题目内容
已知等差数列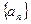 的首项为a,公差为b,等比数列
的首项为a,公差为b,等比数列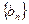 的首项为b,公比为a,其中a、b都是大于1的正整数,且
的首项为b,公比为a,其中a、b都是大于1的正整数,且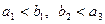 。
。
①求a的值;
②对于任意的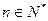 ,总存在
,总存在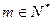 ,使得
,使得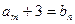 成立,求b;
成立,求b;
③令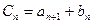 ,问数列
,问数列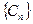 中是否存在连续三项成等比数列,若存在,求出所有成等比数列的连续三项,若不存在,请说明理由。(14分)
中是否存在连续三项成等比数列,若存在,求出所有成等比数列的连续三项,若不存在,请说明理由。(14分)
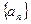 的首项为a,公差为b,等比数列
的首项为a,公差为b,等比数列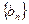 的首项为b,公比为a,其中a、b都是大于1的正整数,且
的首项为b,公比为a,其中a、b都是大于1的正整数,且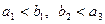 。
。①求a的值;
②对于任意的
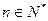 ,总存在
,总存在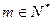 ,使得
,使得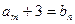 成立,求b;
成立,求b;③令
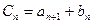 ,问数列
,问数列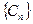 中是否存在连续三项成等比数列,若存在,求出所有成等比数列的连续三项,若不存在,请说明理由。(14分)
中是否存在连续三项成等比数列,若存在,求出所有成等比数列的连续三项,若不存在,请说明理由。(14分)①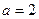 ②
②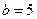 ③这三项依次是18,30,50
③这三项依次是18,30,50
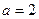 ②
②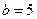 ③这三项依次是18,30,50
③这三项依次是18,30,50解:(1)由已知得: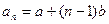 ,
,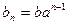 ,由
,由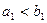 ,
,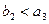 得
得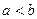 ,
,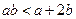 ,∵a,b都是大于1的正整数,∴
,∵a,b都是大于1的正整数,∴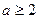 ,
,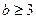 ,又
,又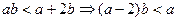 ∵
∵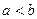 ,∴
,∴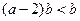 ,∴
,∴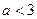 ,∴
,∴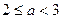 ,∴
,∴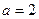 (5分)
(5分)
(2)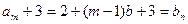 ,∴
,∴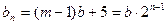 ,∴
,∴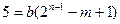 ,∴5一定是b的倍数,∵
,∴5一定是b的倍数,∵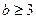 ,∴
,∴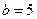 (8分)
(8分)
(3)设数列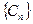 中,
中,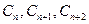 成等比数列,由
成等比数列,由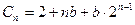 得
得
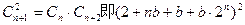
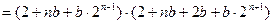
化简得: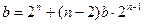 (*) (10分)
(*) (10分)
当n=1时,由(*)式得 b=1,与题意矛盾,当n=2时,由(*)式得 b=4,
即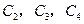 成等比数列,
成等比数列,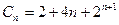 ,∴
,∴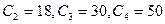 ,
,
当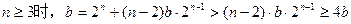 ,这与
,这与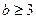 矛盾 (13分)
矛盾 (13分)
综上所述,当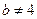 时,不存在连续三项成等比数列,当
时,不存在连续三项成等比数列,当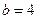 时,数列
时,数列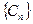 中的第二、三、四项成等比数列,这三项依次是18,30,50 (14分)
中的第二、三、四项成等比数列,这三项依次是18,30,50 (14分)
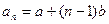 ,
,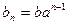 ,由
,由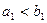 ,
,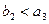 得
得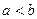 ,
,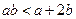 ,∵a,b都是大于1的正整数,∴
,∵a,b都是大于1的正整数,∴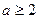 ,
,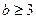 ,又
,又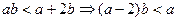 ∵
∵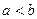 ,∴
,∴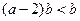 ,∴
,∴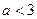 ,∴
,∴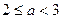 ,∴
,∴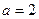 (5分)
(5分)(2)
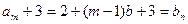 ,∴
,∴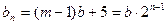 ,∴
,∴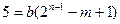 ,∴5一定是b的倍数,∵
,∴5一定是b的倍数,∵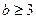 ,∴
,∴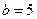 (8分)
(8分)(3)设数列
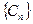 中,
中,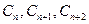 成等比数列,由
成等比数列,由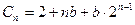 得
得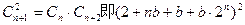
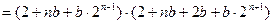
化简得:
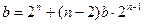 (*) (10分)
(*) (10分)当n=1时,由(*)式得 b=1,与题意矛盾,当n=2时,由(*)式得 b=4,
即
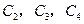 成等比数列,
成等比数列,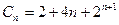 ,∴
,∴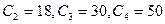 ,
,当
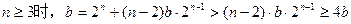 ,这与
,这与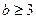 矛盾 (13分)
矛盾 (13分)综上所述,当
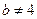 时,不存在连续三项成等比数列,当
时,不存在连续三项成等比数列,当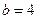 时,数列
时,数列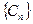 中的第二、三、四项成等比数列,这三项依次是18,30,50 (14分)
中的第二、三、四项成等比数列,这三项依次是18,30,50 (14分)
练习册系列答案
相关题目
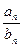 }的前n项和Sn;
}的前n项和Sn;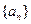 中,
中,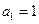 ,
,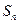 是数列
是数列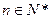 ,有
,有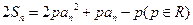
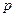 的值;
的值;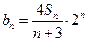 ,求数列
,求数列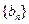 的前n项和
的前n项和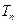 。
。 中,
中,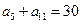 ,
,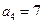 ,则
,则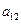 的值为
的值为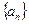 的前
的前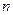 项和为
项和为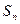 ,且
,且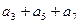 =15,则
=15,则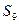 ="( " )
="( " )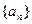 的首项为24,公差为
的首项为24,公差为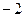 ,则当n= 时,该数列的前n项
,则当n= 时,该数列的前n项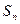 取得最大值.
取得最大值.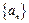 满足
满足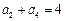 ,
,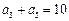 ,则数列{
,则数列{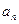 }的公差d=(
}的公差d=(  )
)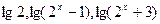 成等差数列,则
成等差数列,则 的值等于( )
的值等于( )
 或
或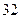
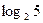
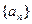 和
和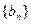 前
前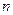 项和分别为
项和分别为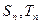 ,且
,且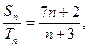 则
则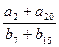 =( )
=( )