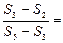题目内容
(本小题满分12分)
设{an}是等差数列,{bn}是各项为正项的等比数列,且a1=b1="1," a3+b5="21," a5+b3=13.
(1)求{an}, {bn}的通项公式;
(2)求数列{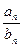 }的前n项和Sn;
}的前n项和Sn;
设{an}是等差数列,{bn}是各项为正项的等比数列,且a1=b1="1," a3+b5="21," a5+b3=13.
(1)求{an}, {bn}的通项公式;
(2)求数列{
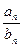 }的前n项和Sn;
}的前n项和Sn;(1)an="2n-1, " bn=2n-1(2)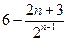
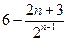
解:(1)设{an}的公差为d,{bn}的公比为q,则依题意有q>0,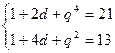
解得d="2,q=2." 所以an="2n-1, " bn=2n-1
((2)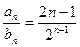 , Sn=1
, Sn=1 +
+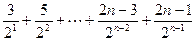
2Sn=2+3+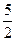
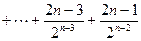
两式相减得:
Sn=2+2(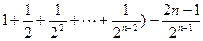 =2+
=2+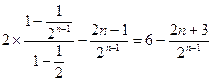
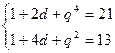
解得d="2,q=2." 所以an="2n-1, " bn=2n-1
((2)
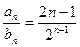 , Sn=1
, Sn=1 +
+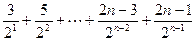
2Sn=2+3+
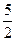
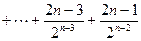
两式相减得:
Sn=2+2(
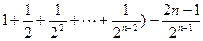 =2+
=2+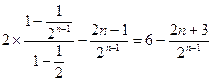

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
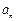 逐月递增且控制在2万件内;
逐月递增且控制在2万件内;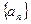 的首项为a,公差为b,等比数列
的首项为a,公差为b,等比数列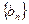 的首项为b,公比为a,其中a、b都是大于1的正整数,且
的首项为b,公比为a,其中a、b都是大于1的正整数,且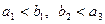 。
。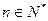 ,总存在
,总存在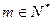 ,使得
,使得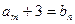 成立,求b;
成立,求b;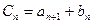 ,问数列
,问数列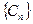 中是否存在连续三项成等比数列,若存在,求出所有成等比数列的连续三项,若不存在,请说明理由。(14分)
中是否存在连续三项成等比数列,若存在,求出所有成等比数列的连续三项,若不存在,请说明理由。(14分)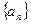 中,
中,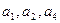 这三项构成等比数列,则公比
这三项构成等比数列,则公比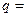
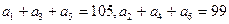 ,则
,则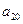 等于_ ____
等于_ ____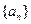 、
、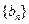 的前
的前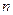 项和的比
项和的比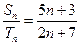 ,则
,则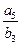 的值是
的值是 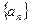 为等差数列,
为等差数列,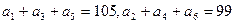 ,则
,则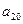 等于 ( )
等于 ( )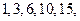 …的递推公式是
…的递推公式是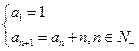
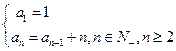
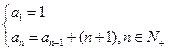
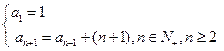
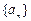 中,
中,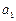 、
、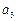 、
、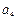 成等比数列,
成等比数列,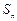 是
是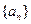 的前n项和,则
的前n项和,则