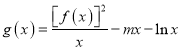题目内容
【题目】若函数![]() 在定义域
在定义域![]() 内的某个区间
内的某个区间![]() 上是增函数,且
上是增函数,且![]() 在
在![]() 上也是增函数,则称
上也是增函数,则称![]() 是
是![]() 上的“完美增函数”.已知
上的“完美增函数”.已知![]() ,
,![]() .
.
(1)判断函数![]() 是否为区间
是否为区间![]() 上的“完美增函数”;
上的“完美增函数”;
(2)若函数![]() 是区间
是区间![]() 上的“完美增函数”,求实数
上的“完美增函数”,求实数![]() 的最大值.
的最大值.
【答案】(1)不是;(2)![]()
【解析】
(1)可根据已知条件分别求出![]() 和
和![]() 在区间
在区间![]() 是不是单调递增函数,再根据给的定义来判断是否为“完美增函数”;
是不是单调递增函数,再根据给的定义来判断是否为“完美增函数”;
(2)利用函数![]() 是区间
是区间![]() 上的“完美增函数”,可得到
上的“完美增函数”,可得到![]() 和
和![]() 在区间
在区间![]() 均为增函数,从而可得到实数
均为增函数,从而可得到实数![]() 的最大值.
的最大值.
(1)由![]() ,则求导得
,则求导得![]() ,
,
所以![]() 在
在![]() 上是增函数;
上是增函数;
又![]() ,则求导得
,则求导得![]() ,
,
当![]() 时,
时,![]() 不恒成立,即
不恒成立,即![]() 在
在![]() 上不是增函数.
上不是增函数.
所以函数![]() 不是区间
不是区间![]() 上的“完美增函数”.
上的“完美增函数”.
(2)因为函数![]() 是区间
是区间![]() 上的“完美增函数”,
上的“完美增函数”,
所以![]() 和
和![]() 在区间
在区间![]() 均为增函数,
均为增函数,
由![]() ,则求导得
,则求导得![]() ,
,
即![]() 在区间
在区间![]() 上单调递增.
上单调递增.
又![]() ,求导得
,求导得![]() ,
,
若![]() ,则
,则![]() ,解得
,解得![]() ,
,
即当![]() 时,
时,![]() 恒成立,
恒成立,![]() 在
在![]() 上单调递增.
上单调递增.
于是实数![]() 的最大值为
的最大值为![]() .
.

【题目】在贯彻中共中央国务院关于精准扶贫政策的过程中,某单位定点帮扶100户贫困户.工作组对这100户村民的贫困状况和家庭成员受教育情况进行了调查:甲村55户贫困村民中,家庭成员接受过中等及以上教育的只有10户,乙村45户贫困村民中,家庭成员接受过中等及以上教育的有20户.
(1)完成下面的列联表,并判断是否有99.5%的把握认为贫困与接受教育情况有关;
家庭成员接受过中等以下 教育的户数 | 家庭成员接受过中等及以上 教育的户数 | 合计 | |
甲村贫困户数 | |||
乙村贫困户数 | |||
合计 |
(2)在被帮扶的100户贫困户中,按分层抽样的方法从家庭成员接受过中等及以上教育的贫困户中抽取6户,再从这6户中采用简单随机抽样的方法随机抽取2户,求这2户中甲、乙两村恰好各1户的概率.
参考公式与数据: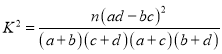 ,其中
,其中![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |