题目内容
(2013•广东模拟)设函数f(x)=3sin(ωx+φ)(ω>0,-
<φ<
)的图象关于直线x=
π对称,它的周期是π,则( )
| π |
| 2 |
| π |
| 2 |
| 2 |
| 3 |
分析:由题意通过周期与对称轴,分别求出ω,与φ,推出函数的解析式,然后逐个验证选项,判断正误即可.
解答:解:因为函数的周期为π,所以ω=2,又函数图象关于直线x=
π对称,
所以由f(x)=3sin(2x+φ)(ω>0,-
<φ<
),
可知2×
π+φ=kπ+
,φ=kπ-
,-
<φ<
,
所以k=1时φ=
.
函数的解析式为:f(x)=3sin(2x+
).当x=0时f(0)=
,所以A不正确.
当
<x<
,2x+
∈[
,
],函数不是单调减函数,B不正确;
当x=
时f(x)=0.函数的一个对称中心是(
,0)正确;
f(x)的图象向右平移|φ|个单位得到函数y=3sin(ωx+φ-ωφ)的图象,不是函数y=3sinωx的图象,D不正确;
故选C.
| 2 |
| 3 |
所以由f(x)=3sin(2x+φ)(ω>0,-
| π |
| 2 |
| π |
| 2 |
可知2×
| 2 |
| 3 |
| π |
| 2 |
| 5π |
| 6 |
| π |
| 2 |
| π |
| 2 |
所以k=1时φ=
| π |
| 6 |
函数的解析式为:f(x)=3sin(2x+
| π |
| 6 |
| 3 |
| 2 |
当
| π |
| 12 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| 3π |
| 2 |
当x=
| 5π |
| 12 |
| 5π |
| 12 |
f(x)的图象向右平移|φ|个单位得到函数y=3sin(ωx+φ-ωφ)的图象,不是函数y=3sinωx的图象,D不正确;
故选C.
点评:本题考查三角函数的解析式的求法,函数的基本性质的应用,考查计算能力.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
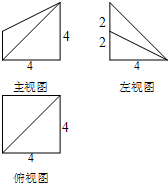 (2013•广东模拟)一几何体的三视图如图所示,则这个几何体的体积为
(2013•广东模拟)一几何体的三视图如图所示,则这个几何体的体积为