题目内容
16.若等腰△ABC一底角的正弦值为$\frac{1}{3}$,则顶角A的正弦值是$\frac{4\sqrt{2}}{9}$.分析 根据三角形的诱导公式先求出cos∠BAD=sinB=$\frac{1}{3}$,然后利用倍角公式进行求解即可.
解答 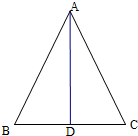 解:设sinB=$\frac{1}{3}$,则cos∠BAD=sinB=$\frac{1}{3}$,
解:设sinB=$\frac{1}{3}$,则cos∠BAD=sinB=$\frac{1}{3}$,
则cosA=2cos2∠BAD-1=2×$(\frac{1}{3})^{2}$-1=$\frac{2}{9}-1$=$-\frac{7}{9}$,
则sinA=$\sqrt{1-co{s}^{2}A}$=$\sqrt{1-(-\frac{7}{9})^{2}}=\sqrt{\frac{32}{81}}$=$\frac{4\sqrt{2}}{9}$,
故答案为:$\frac{4\sqrt{2}}{9}$.
点评 本题主要考查三角诱导公式以及倍角公式的应用,要求熟练掌握相应的公式.

练习册系列答案
相关题目