题目内容
【题目】已知函数f(x)=|x-1|.
(I) 解不等式f(2x)+f(x+4)≥8;
(II) 若|a|<1,|b|<1,a≠0,求证: ![]() >
>![]() .
.
【答案】(Ⅰ) ![]()
(II)证明见解析
【解析】
(1)根据![]() 的分段函数形式,分类讨论求得不等式f(2x)+f(x+4)≥8的解集;(2)要证的不等式即
的分段函数形式,分类讨论求得不等式f(2x)+f(x+4)≥8的解集;(2)要证的不等式即![]() ,根据|a|<1,|b|<1,可得
,根据|a|<1,|b|<1,可得![]() ,从而得到所证的不等式成立。
,从而得到所证的不等式成立。
(Ⅰ)f(2x)+f(x+4)=|2x-1|+|x+3|=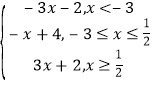
当x<-3时,由-3x-2≥8,解得x≤![]() ;
;
当-3≤x<![]() 时,-x+4≥8无解;
时,-x+4≥8无解;
当x≥![]() 时,由3x+2≥8,解得x≥2.
时,由3x+2≥8,解得x≥2.
所以不等式f(2x)+f(x+4)≥8的解集为![]()
(II)证明:![]() >
>![]() 等价于f(ab)>|a|
等价于f(ab)>|a|![]() ,即|ab-1|>|a-b|.
,即|ab-1|>|a-b|.
因为|a|<1,|b|<1,
所以|ab-1|2-|a-b|2=(a2b2-2ab+1)-(a2-2ab+b2)=(a2-1)(b2-1)>0,
所以|ab-1|>|a-b|.故所证不等式成立.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目