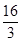题目内容
设函数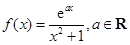 .
.
(Ⅰ)当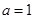 时,求曲线
时,求曲线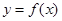 在点
在点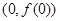 处的切线方程;
处的切线方程;
(Ⅱ)求函数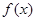 单调区间.
单调区间.
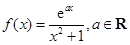 .
.(Ⅰ)当
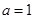 时,求曲线
时,求曲线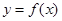 在点
在点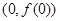 处的切线方程;
处的切线方程;(Ⅱ)求函数
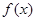 单调区间.
单调区间.解:因为
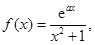 所以
所以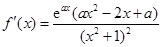 .
.(Ⅰ)当
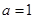 时,
时,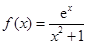 ,
,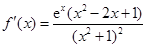 ,
,所以
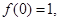
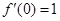 .
.所以曲线
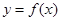 在点
在点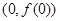 处的切线方程为
处的切线方程为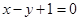 . ……………4分
. ……………4分(Ⅱ)因为
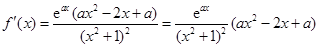 , ……………5分
, ……………5分(1)当
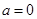 时,由
时,由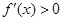 得
得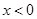 ;由
;由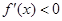 得
得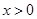 .[
.[所以函数
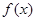 在区间
在区间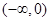 单调递增, 在区间
单调递增, 在区间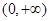 单调递减. ……………6分
单调递减. ……………6分(2)当
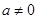 时,设
时,设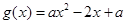 ,方程
,方程 的判别式
的判别式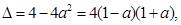 ……………7分
……………7分①当
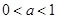 时,此时
时,此时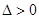 .
.由
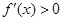 得
得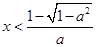 ,或
,或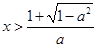 ;
;由
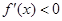 得
得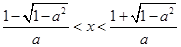 .
.所以函数
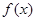 单调递增区间是
单调递增区间是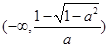 和
和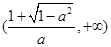 ,
, 单调递减区间
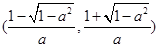 . ……………9分
. ……………9分②当
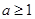 时,此时
时,此时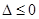 .所以
.所以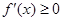 ,
,所以函数
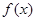 单调递增区间是
单调递增区间是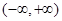 . ……………10分
. ……………10分③当
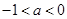 时,此时
时,此时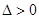 .
.由
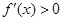 得
得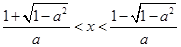 ;
;由
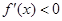 得
得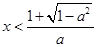 ,或
,或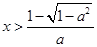 .
.所以当
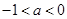 时,函数
时,函数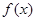 单调递减区间是
单调递减区间是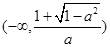 和
和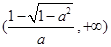 ,
, 单调递增区间
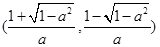 . ……………12分
. ……………12分④当
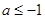 时,此时
时,此时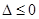 ,
,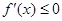 ,所以函数
,所以函数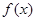 单调递减区间是
单调递减区间是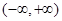 .
.略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
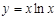 在
在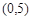 上是( ).
上是( ).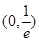 上单调递减,在
上单调递减,在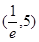 上单调递增.
上单调递增.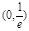 上单调递增,在
上单调递增,在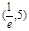 上单调递减;
上单调递减;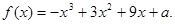
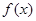 的单调减区间;
的单调减区间;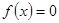 有三个不同的实根,求
有三个不同的实根,求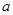 的取值范围;
的取值范围; ,有
,有 ,
, ,且
,且 时,
时, ,
, ,则
,则 时( )
时( )
 ,
,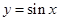 在
在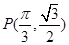 处的切线斜率是 .
处的切线斜率是 . 在x=x0处可导,且
在x=x0处可导,且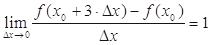 ,则
,则

 ,则
,则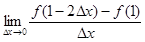 =( )
=( )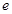
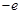
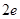
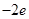

 ,则a的值是( )
,则a的值是( )