题目内容
已知函数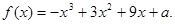
(1)求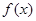 的单调减区间;
的单调减区间;
(2)若方程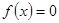 有三个不同的实根,求
有三个不同的实根,求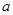 的取值范围;
的取值范围;
(3)若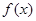 在区间[-2,2]上的最大值为20,求它在该区间上的最小值.
在区间[-2,2]上的最大值为20,求它在该区间上的最小值.
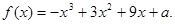
(1)求
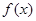 的单调减区间;
的单调减区间;(2)若方程
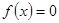 有三个不同的实根,求
有三个不同的实根,求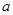 的取值范围;
的取值范围;(3)若
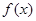 在区间[-2,2]上的最大值为20,求它在该区间上的最小值.
在区间[-2,2]上的最大值为20,求它在该区间上的最小值.解:(1)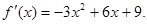 令
令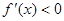 ,解得
,解得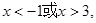 ……………2分
……………2分
所以函数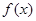 的单调递减区间为
的单调递减区间为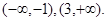 …………………3分
…………………3分
(2)由(1)可知,函数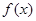 的单调递减区间为
的单调递减区间为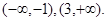 ,函数
,函数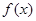 的单调递增区间为
的单调递增区间为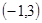 ,所以
,所以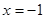 是极小值点,
是极小值点,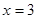 是极大值点, …………………………4分
是极大值点, …………………………4分
所以,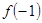 是极小值且
是极小值且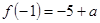 ,
,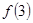 是极大值且
是极大值且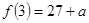 …………5分
…………5分
方程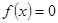 有三个不同的实根,即
有三个不同的实根,即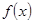 的图象与
的图象与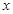 轴有三个交点,需满足
轴有三个交点,需满足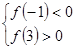
 解得:
解得: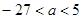 …………………………7分
…………………………7分
(3)因为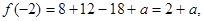
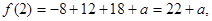
所以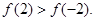 …………………………………8分
…………………………………8分
因为在(-1,3)上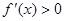 ,所以
,所以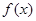 在[-1,2]上单调递增,又由于
在[-1,2]上单调递增,又由于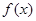 在[-2,-1]上单调递减,因此
在[-2,-1]上单调递减,因此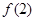 和
和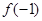 分别是
分别是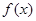 在区间
在区间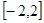 上的最大值和最小值.…… 10分
上的最大值和最小值.…… 10分
于是有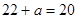 ,解得
,解得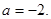 ……………………………………11分
……………………………………11分
故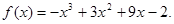 因此
因此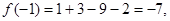
即函数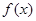 在区间
在区间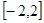 上的最小值为-7. ……………………………………12分
上的最小值为-7. ……………………………………12分
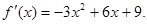 令
令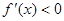 ,解得
,解得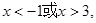 ……………2分
……………2分所以函数
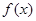 的单调递减区间为
的单调递减区间为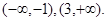 …………………3分
…………………3分(2)由(1)可知,函数
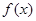 的单调递减区间为
的单调递减区间为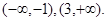 ,函数
,函数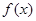 的单调递增区间为
的单调递增区间为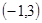 ,所以
,所以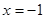 是极小值点,
是极小值点,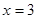 是极大值点, …………………………4分
是极大值点, …………………………4分所以,
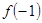 是极小值且
是极小值且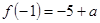 ,
,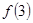 是极大值且
是极大值且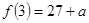 …………5分
…………5分方程
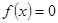 有三个不同的实根,即
有三个不同的实根,即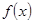 的图象与
的图象与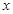 轴有三个交点,需满足
轴有三个交点,需满足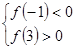
 解得:
解得: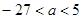 …………………………7分
…………………………7分(3)因为
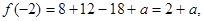
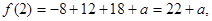
所以
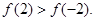 …………………………………8分
…………………………………8分因为在(-1,3)上
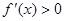 ,所以
,所以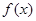 在[-1,2]上单调递增,又由于
在[-1,2]上单调递增,又由于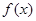 在[-2,-1]上单调递减,因此
在[-2,-1]上单调递减,因此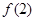 和
和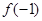 分别是
分别是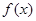 在区间
在区间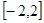 上的最大值和最小值.…… 10分
上的最大值和最小值.…… 10分于是有
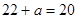 ,解得
,解得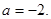 ……………………………………11分
……………………………………11分故
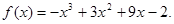 因此
因此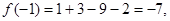
即函数
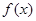 在区间
在区间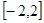 上的最小值为-7. ……………………………………12分
上的最小值为-7. ……………………………………12分略

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
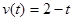 ,质点作直线运动,则此质点体在
,质点作直线运动,则此质点体在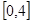 时间内的路程为 ( )
时间内的路程为 ( )
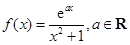 .
.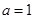 时,求曲线
时,求曲线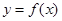 在点
在点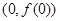 处的切线方程;
处的切线方程;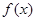 单调区间.
单调区间.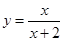 在点(-1,-1)处的切线方程为( )
在点(-1,-1)处的切线方程为( )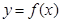 的图像(如图所示)过点
的图像(如图所示)过点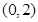 、
、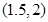 和点
和点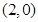 ,且函数图像关于点
,且函数图像关于点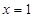 和
和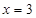 及
及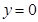 是它的渐近线.现要求根据给出的函数图像研究函数
是它的渐近线.现要求根据给出的函数图像研究函数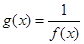 的相关性质与图像,
的相关性质与图像,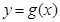 的定义域、值域及单调递增区间;
的定义域、值域及单调递增区间;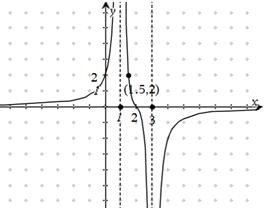
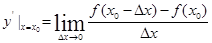



 在
在 处的切线与y轴的交点为 。
处的切线与y轴的交点为 。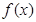 =ln(x+
=ln(x+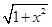 ),则
),则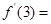
 _________.
_________.