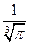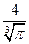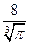题目内容
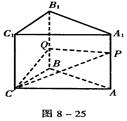
如图8-25,在三棱柱的侧棱A1A和B1B上各有一动点P,Q,且满足A1P=BQ,过P、Q、C三点的截面把棱柱分成两部分,则其体积之比为( )

| A.3∶1 | B.2∶1 | C.4∶1 | D.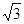 ∶1 ∶1 |
B
解:设三棱柱ABC-A1B1C1的体积为V.
∵侧棱AA1和BB1上各有一动点P,Q满足A1P=BQ,
∴四边形PQBA与四边形PQB1A1的面积相等.
故四棱椎C-PQBA的体积等于三棱锥C-ABA1的体积等于
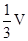 .
.则几何体CPQ-C1B1A1的体积等于
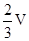 .
.故过P、Q、C三点的截面把棱柱分成两部分,则其体积比为2:1.
故选B.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
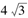 ,BC=
,BC=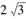 ,且矩形从CD的顶点都在半径为R的球O的球面上,若四棱锥O -ABCD的体积为8,则球O的半径R=
,且矩形从CD的顶点都在半径为R的球O的球面上,若四棱锥O -ABCD的体积为8,则球O的半径R=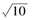
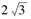
 为圆柱形木块底面的圆心,
为圆柱形木块底面的圆心,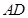 是底面圆的一条弦,优弧
是底面圆的一条弦,优弧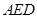 的长为底面圆的周长的
的长为底面圆的周长的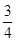 .过
.过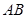 的平面将木块剖开,得到截面
的平面将木块剖开,得到截面 ,已知四边形
,已知四边形 .
.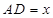 ,求⊙
,求⊙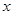 表示);
表示);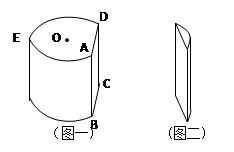
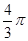
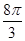


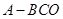 ,
,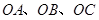 两两垂直且长度均为6,长为2的线段
两两垂直且长度均为6,长为2的线段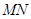 的一个端点
的一个端点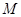 在棱
在棱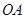 上运动,另一个端点
上运动,另一个端点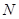 在
在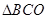 内运动(含边界),则
内运动(含边界),则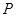 的轨迹与三棱锥的面所围成的几何体的体积为
的轨迹与三棱锥的面所围成的几何体的体积为 
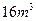 的圆柱形封闭容器,要使所用的材料最省,底面直径为 ( )
的圆柱形封闭容器,要使所用的材料最省,底面直径为 ( )