题目内容
如图,矩形 中,
中,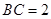 ,
, ,
,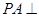 平面
平面 ,
,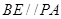 ,
,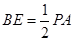 ,
,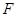 为
为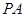 的中点.
的中点.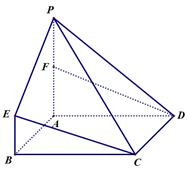
(1)求证: 平面
平面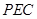 .
.
(2)若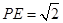 ,求平面
,求平面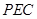 与平面
与平面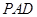 所成锐二面角的余弦值.
所成锐二面角的余弦值.
(1)证明线面平行,关键是证明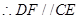 线线平行,然后结合判定定理得到。
线线平行,然后结合判定定理得到。
(2)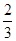
解析试题分析:(1)连接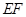
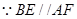 ,
,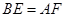
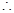 四边形
四边形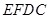 为平行四边形
为平行四边形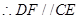
又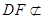 平面
平面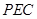
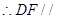 平面
平面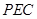 3分
3分
(2)以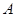 为原点,AB、AD、AP为x、y、z方向建立空间直角坐标系
为原点,AB、AD、AP为x、y、z方向建立空间直角坐标系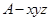 .
.
易得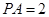 ,则
,则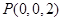 、
、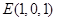 、
、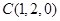 5分
5分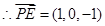 ,
,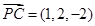 ,
,
由此可求得平面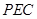 的法向量
的法向量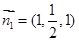 7分
7分
又平面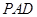 的法向量
的法向量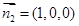
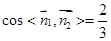 ,
,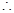 两平面所成锐二面角的余弦值为
两平面所成锐二面角的余弦值为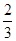 . 10分
. 10分
考点:空间中线面平行,以及二面角的平面角
点评:主要是考查了线面平行的判定以及二面角的平面角的求解,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
经过点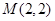 且在两轴上截距相等的直线是( )
且在两轴上截距相等的直线是( )
A.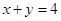 | B.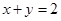 |
C.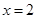 或 或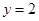 | D.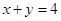 或 或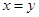 |
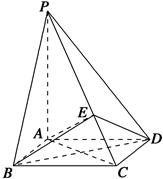
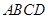 -
-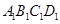 中,
中,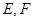 分别为
分别为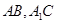 的中点. 应用空间向量方法求解下列问题.
的中点. 应用空间向量方法求解下列问题. 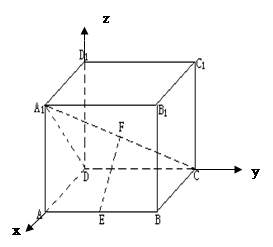
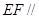 平面
平面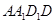 ;
;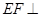 平面
平面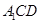 .
.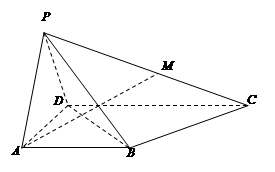
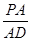 多大时,AM⊥平面PDB可能成立?
多大时,AM⊥平面PDB可能成立?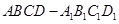 是正方体,其中
是正方体,其中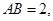
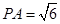
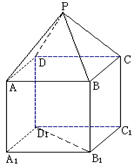
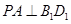 ;
;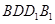 所成的锐二面角
所成的锐二面角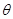 的余弦值;
的余弦值;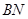 ⊥平面
⊥平面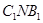 (2)求平面
(2)求平面 与平面
与平面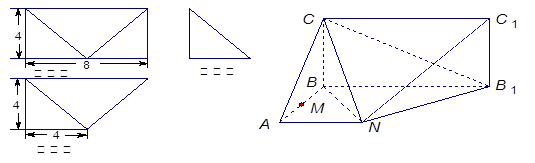
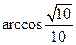 ,求BD的长度.(15分)
,求BD的长度.(15分)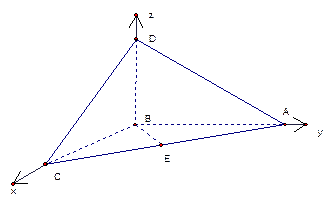
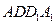 和三棱锥
和三棱锥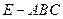 组合而成,点
组合而成,点 、
、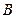 、
、 在圆
在圆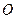 的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图3所示,其中
的圆周上,其正(主)视图、侧(左)视图的面积分别为10和12,如图3所示,其中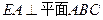 ,
,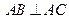 ,
,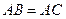 ,
,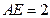 .
.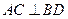 ;
;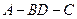 的平面角的大小.
的平面角的大小.