题目内容
对a、b∈R,记max{a,b}=
,函数f(x)=max{|x+1|,|2x+5|}(x∈R).
(1)求f(0),f(-3);
(2)作出f(x)的图象,并写出f(x)的单调区间;
(3)若关于x的方程f(x)=m有且仅有两个不等的解,求实数m的取值范围.
|
(1)求f(0),f(-3);
(2)作出f(x)的图象,并写出f(x)的单调区间;
(3)若关于x的方程f(x)=m有且仅有两个不等的解,求实数m的取值范围.
分析:(1)根据题中所给条件通过比较|x+1|、|2x+5|哪一个更大,先画出f(x)的图象,再求出f(x)当x=0或x=-3时的函数值,
(2)结合图象写出f(x)的单调区间.
(3)先据此函数的图象得到f(x)min=f(-2)=1,然后根据图象交点的情况即可求出实数m的取值范围.
(2)结合图象写出f(x)的单调区间.
(3)先据此函数的图象得到f(x)min=f(-2)=1,然后根据图象交点的情况即可求出实数m的取值范围.
解答: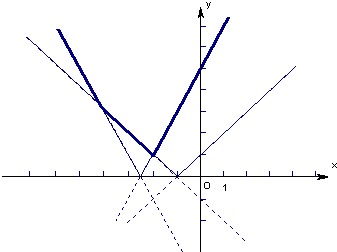 解:f(x)图象如图中粗线所示…(4分)
解:f(x)图象如图中粗线所示…(4分)
(1)f(0)=max{1,5}=5,f(-3)=max{2,1}=2;…(4分)
(2)由图象可知f(x)的单调减区间为(-∞,-2],单调增区间为[-2,+∞);…(3分)
(3)f(x)min=f(-2)=1,由f(x)图象可知当m>1时方程f(x)=m有且仅有两个不等的解.…(3分)
 解:f(x)图象如图中粗线所示…(4分)
解:f(x)图象如图中粗线所示…(4分)(1)f(0)=max{1,5}=5,f(-3)=max{2,1}=2;…(4分)
(2)由图象可知f(x)的单调减区间为(-∞,-2],单调增区间为[-2,+∞);…(3分)
(3)f(x)min=f(-2)=1,由f(x)图象可知当m>1时方程f(x)=m有且仅有两个不等的解.…(3分)
点评:本题主要考查函数的最值及其几何意义.这种先给出定义,让根据条件求解析式是经常考到点.数形结合是关键.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目