题目内容
对a，b∈R，记max（a，b）=
，函数f（x）=max（|x+1|，-x2+1）的最小值是
|
0
0
．分析：在解答时应先根据|x+1|和-x2+1的大小关系，结合新定义给出函数f（x）的图象即可获得问题的解答．
解答：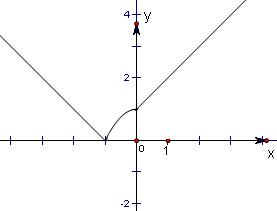
解：分别画出函数y=|x+1|和y=-x2+1的图象，由于f（x）=max（|x+1|，-x2+1）表示上述两个函数值中最大者，
故函数f（x）=max（|x+1|，-x2+1）的简图所图所示．其图象如右，
则fmin（x）=f（-1）=0．
故答案为：0．
解：分别画出函数y=|x+1|和y=-x2+1的图象，由于f（x）=max（|x+1|，-x2+1）表示上述两个函数值中最大者，故函数f（x）=max（|x+1|，-x2+1）的简图所图所示．其图象如右，
则fmin（x）=f（-1）=0．
故答案为：0．
点评：本题考查新定义函数的理解和分段函数的解析式求法及其图象的作法等问题，属于中档题．在解答过程当中充分考查了同学们的创新思维，培养了良好的数学素养．
练习册系列答案
名校课堂系列答案
相关题目