题目内容
对a、b∈R,记max{a,b}=
,函数f(x)=max{|x+1|,|x-2|}(x∈R).
(1)作出f(x)的图象,并写出f(x)的解析式;
(2)若函数h(x)=x2-λf(x)在(-∞,-1]上是单调函数,求λ的取值范围.
(3)当x∈[1,+∞)时,函数h(x)=x2-λf(x)的最小值为2,求λ的值.
|
(1)作出f(x)的图象,并写出f(x)的解析式;
(2)若函数h(x)=x2-λf(x)在(-∞,-1]上是单调函数,求λ的取值范围.
(3)当x∈[1,+∞)时,函数h(x)=x2-λf(x)的最小值为2,求λ的值.
分析:(1)根据|x+1|和|x-2|的大小关系,结合新定义画函数的图象,写出函数f(x)的解析式故f(x)=
(2)h(x)=x2-λf(x)=
若在(-∞,-1]上是单调函数,则要求第二段在(-∞,-1]上是单调函数.
(3)当x∈[1,+∞)时,h(x)=x2-λ(x+1),利用二次函数图象与性质求其最小值,得出关于λ的方程求解.注意分类讨论.
|
(2)h(x)=x2-λf(x)=
|
(3)当x∈[1,+∞)时,h(x)=x2-λ(x+1),利用二次函数图象与性质求其最小值,得出关于λ的方程求解.注意分类讨论.
解答:解:解:由|x+1|≥|x-2|⇒(x+1)2≥(x-2)2⇒x≥
,故f(x)=
=
其图象如右,其图象如右,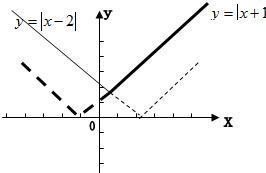
(2)h(x)=x2-λf(x)=
若在(-∞,-1]上是单调函数,则要求第二段在(-∞,-1]上是单调函数,对称轴x=-
≥-1,解得λ≤2
(3)当x∈[1,+∞)时,h(x)=x2-λ(x+1)
对称轴x=
,
当
≤1,即λ≤2时,h(x)在[1,+∞)上单调递增,最小值为h(1)=1-2λ=2,得λ=-
当
>1,即λ>2时,最小值为h(
)=
=2,此时无解
综上所述,λ=-
| 1 |
| 2 |
|
|
其图象如右,其图象如右,

(2)h(x)=x2-λf(x)=
|
若在(-∞,-1]上是单调函数,则要求第二段在(-∞,-1]上是单调函数,对称轴x=-
| λ |
| 2 |
(3)当x∈[1,+∞)时,h(x)=x2-λ(x+1)
对称轴x=
| λ |
| 2 |
当
| λ |
| 2 |
| 1 |
| 2 |
当
| λ |
| 2 |
| λ |
| 2 |
| -4λ-λ2 |
| 4 |
综上所述,λ=-
| 1 |
| 2 |
点评:本题考查分段函数的单调性,最大值,转化为二次函数问题.要具有阅读理解能力、转化计算能力、分类讨论的思想方法.

练习册系列答案
相关题目