题目内容
10.在坐标平面上,不等式组$\left\{\begin{array}{l}{y≥x-1}\\{y≤-3|x|+1}\end{array}\right.$所表示的平面区域的面积为( )| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | 2 |
分析 作出不等式组对应的平面区域,根据对应图形,求出对应的面积即可.
解答 解:作出不等式组对应的平面区域,
则A(0,1),A到直线y=x-1,即x-y-1=0的距离d=$\frac{|-1-1|}{\sqrt{2}}=\frac{2}{\sqrt{2}}=\sqrt{2}$,
由$\left\{\begin{array}{l}{y=x-1}\\{y=-3x+1}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=-\frac{1}{2}}\end{array}\right.$,即C($\frac{1}{2}$,-$\frac{1}{2}$),
由$\left\{\begin{array}{l}{y=x-1}\\{y=3x+1}\end{array}\right.$,得$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$,即B(-1,-2),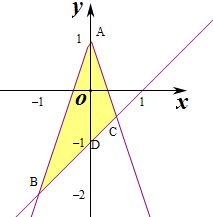
则|BC|=$\sqrt{(-1-\frac{1}{2})^{2}+(-2+\frac{1}{2})^{2}}$=$\frac{3\sqrt{2}}{2}$,
则△ABC的面积S=$\frac{1}{2}|BC|•d=\frac{1}{2}×\frac{3\sqrt{2}}{2}×\sqrt{2}$=$\frac{3}{2}$,
故选:B
点评 本题二元一次不等式组表示平面区域,根据条件作出平面区域,根据三角形的面积公式是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.函数f(x)=Asin(ωx+φ)+b图象的一部分如图所示,则f(x)的解析式为( )


| A. | y=sin2x-2 | B. | y=2cos3x-1 | C. | y=sin(2x-$\frac{π}{5}$)+1 | D. | y=1-sin(2x-$\frac{π}{5}$) |
2.某多面体的三视图如图所示,则该多面体的各条棱中,最长的棱的长度为( )


| A. | 2$\sqrt{5}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{5}$ | D. | 2 |
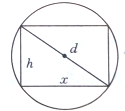 横截面为矩形的横梁的强度同它的断面高的平方与宽的积成正比,要将直径为d的圆木锯成强度最大的横梁,断面的宽的和高度应是多少?
横截面为矩形的横梁的强度同它的断面高的平方与宽的积成正比,要将直径为d的圆木锯成强度最大的横梁,断面的宽的和高度应是多少? 如图所示是函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的一段图象.
如图所示是函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的一段图象.